
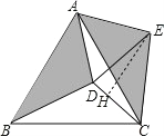
【题目】如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,求∠CDE的正切值.

【答案】3![]()
【解析】
先根据等边三角形的性质得AB=AC,∠BAC=60°,再根据旋转的性质得到AD=AE=5,∠DAE=∠BAC=60°,CE=BD=6,即可判定△ADE为等边三角形,得到DE=AD=5,过点E作EH⊥CD于H,如图,设DH=x,则CH=4-x,利用勾股定理得到52-x2=62-(4-x)2,解得x=![]() ,再计算出EH,然后利用正切的定义求解.
,再计算出EH,然后利用正切的定义求解.
∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
∵将△ABD绕A点逆时针旋转得到△ACE,
∴AD=AE=5,∠DAE=∠BAC=60°,CE=BD=6,
∴△ADE为等边三角形,
∴DE=AD=5,
过点E作EH⊥CD于H,如图,设DH=x,则CH=4-x,
在Rt△DHE中,EH2=52-x2
在Rt△CHE中,EH2=62-(4-x)2,
∴52-x2=62-(4-x)2,
解得x=![]() ,
,
∴EH=![]()
在Rt△DHE中,tan∠CDE=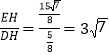
即∠CDE的正切值是![]()


科目:初中数学 来源: 题型:
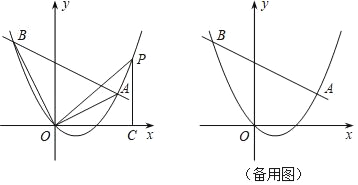
【题目】如图,在平面直角坐标系中,直线y=kx﹣4k+4与抛物线y=![]() x2﹣x交于A、B两点.
x2﹣x交于A、B两点.
(1)直线总经过定点,请直接写出该定点的坐标;
(2)点P在抛物线上,当k=﹣![]() 时,解决下列问题:
时,解决下列问题:
①在直线AB下方的抛物线上求点P,使得△PAB的面积等于20;
②连接OA,OB,OP,作PC⊥x轴于点C,若△POC和△ABO相似,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
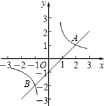
【题目】如图,直线y=x+m与双曲线![]() 相交于A(2,1)、B两点.
相交于A(2,1)、B两点.
(1)求m及k的值;
(2)求出点B的坐标;并直接写出x取何值时,![]() ;
;
(3)P为直线x=![]() 上一点,当△ APB的面积为6时,请直接写出点P的坐标.
上一点,当△ APB的面积为6时,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
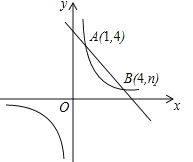
【题目】(10分)如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.
(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
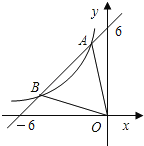
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象相交于A,B两点,且与坐标轴的交点为(﹣6,0),(0,6),点B的横坐标为﹣4.
的图象相交于A,B两点,且与坐标轴的交点为(﹣6,0),(0,6),点B的横坐标为﹣4.
(1)试确定反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出不等式![]() 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与B港口之间的距离即CB的长(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高![]() 米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心
米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心![]() 米.
米.

(1)请你建立适当的直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行“传承好家风”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了它们的成绩,并绘制了如图不完整的两幅统计图表.
征文比赛成绩频数分布表
分数段 | 频数 | 频率 |
60≤m<70 | 38 | 0.38 |
70≤m<80 | a | 0.32 |
80≤m<90 | b | c |
90≤m≤100 | 10 | 0.1 |
合计 | 1 |
请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中c的值是_____;
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com