
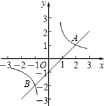
【题目】如图,直线y=x+m与双曲线![]() 相交于A(2,1)、B两点.
相交于A(2,1)、B两点.
(1)求m及k的值;
(2)求出点B的坐标;并直接写出x取何值时,![]() ;
;
(3)P为直线x=![]() 上一点,当△ APB的面积为6时,请直接写出点P的坐标.
上一点,当△ APB的面积为6时,请直接写出点P的坐标.
【答案】(1)m=-1,k=2 ;(2)B(-1,-2),-1<x <0或x>2;(3)(![]() )或(
)或(![]() ,-
,-![]() ).
).
【解析】
(1)把A的坐标分别代入两函数的解析式即可求出答案;
(2)解由两函数组成的方程组,求出方程组的解,即可得出B的坐标;结合图象和两交点的横坐标即可得出答案;
(3)设直线x=![]() 与直线AB相交于点D(
与直线AB相交于点D(![]() ,y),则可求出y的值,得到D的坐标.设P(
,y),则可求出y的值,得到D的坐标.设P(![]() ,b),由S△ABP= S△PAD +S△PDB =
,b),由S△ABP= S△PAD +S△PDB =![]() PD(
PD(![]() )=6,解方程即可得到结论.
)=6,解方程即可得到结论.
(1)∵把A(2,1)代入y=x+m得:1=2+m,∴m=﹣1.
∵把A(2,1)代入y![]() 得:1
得:1![]() ,∴k=2;
,∴k=2;
(2)∵解由y=x﹣1和y![]() 组成的方程组
组成的方程组 得:
得:![]() .
.
又∵A(2,1),∴B的坐标是(﹣1,﹣2);由图像可知:![]() 时x的取值范围是﹣1<x<0或x>2.
时x的取值范围是﹣1<x<0或x>2.
(3)设直线x=![]() 与直线AB相交于点D(
与直线AB相交于点D(![]() ,y),则y=
,y),则y=![]() ,∴D(
,∴D(![]() ,
,![]() ).
).
设P(![]() ,b),则S△ABP= S△PAD +S△PDB =
,b),则S△ABP= S△PAD +S△PDB =![]() PD(
PD(![]() )=6,∴
)=6,∴![]() ,解得:b=
,解得:b=![]() 或b=
或b=![]() ,∴P的坐标为(
,∴P的坐标为(![]() )或(
)或(![]() ,
,![]() ).
).



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
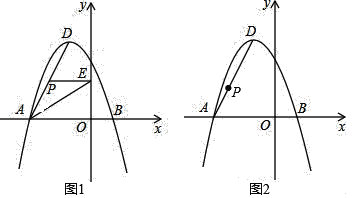
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+3经过A(﹣3,0)、B(1,0)两点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合).
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如图1,过点P作PE⊥y轴于点E.求△PAE面积S的最大值;
(3)如图2,抛物线上是否存在一点Q,使得四边形OAPQ为平行四边形?若存在求出Q点坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具商店销售功能相同的A、B两种品牌的计算器,购买2个A品牌和3个B品牌的计算器共需156元;购买3个A品牌和1个B品牌的计算器共需122元.
(1)求这两种品牌计算器的单价;
(2)学校开学前夕,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的八折销售,B品牌计算器超出5个的部分按原价的七折销售,设购买x个A品牌的计算器需要y1元,购买x(x>5)个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;
(3)当需要购买50个计算器时,买哪种品牌的计算器更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“灵”、“秀”、“黄”、“冈”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,球上的汉字刚好是“黄”的概率为多少?
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图的方法,求出甲取出的两个球上的汉字恰能组成“灵秀”或“黄冈”(汉字不分先后顺序)的概率![]() ;
;
(3)乙从中任取一球,记下汉字后再放回袋中,然后再从中任取一球,记乙取出的两个球上的汉字恰能组成“灵秀”或“黄冈”(汉字不分先后顺序)的概率为![]() ,请直接写出
,请直接写出![]() 的值,并比较
的值,并比较![]() ,
,![]() 的大小.(2+3+2=7)
的大小.(2+3+2=7)
查看答案和解析>>
科目:初中数学 来源: 题型:
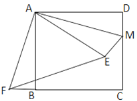
【题目】如图,在正方形ABCD中,点M在CD的边上,且DM=2,ΔAEM与ΔADM关于AM所在的直线对称,将ΔADM按顺时针方向绕点A旋转90°得到ΔABF,连接EF,已知线段EF的长为![]() ,则正方形ABCD的边长为_____
,则正方形ABCD的边长为_____
查看答案和解析>>
科目:初中数学 来源: 题型:
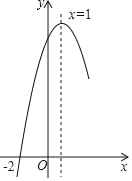
【题目】抛物线y=ax2+bx+c经过点(﹣2,0),且对称轴为直线x=1,其部分图象如图所示.对于此抛物线有如下四个结论:
①ac>0;②16a+4b+c=0;③若m>n>0,则x=1+m时的函数值大于x=1﹣n时的函数值;④点(﹣![]() ,0)一定在此抛物线上.其中正确结论的序号是( )
,0)一定在此抛物线上.其中正确结论的序号是( )
A. ①②B. ②③C. ②④D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,求∠CDE的正切值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】临近期末考试,心理专家建议考生可通过以下四种方式进行考前减压:![]() .享受美食,
.享受美食,![]() .交流谈心,
.交流谈心,![]() .体育锻炼,
.体育锻炼,![]() .欣赏艺术.
.欣赏艺术.
(1)随机采访一名九年级考生,选择其中某一种方式,他选择“享受美食”的概率是 .
(2)同时采访两名九年级考生,请用画树状图或列表的方法求他们中至少有一人选择“欣赏艺术”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com