
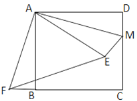
【题目】如图,在正方形ABCD中,点M在CD的边上,且DM=2,ΔAEM与ΔADM关于AM所在的直线对称,将ΔADM按顺时针方向绕点A旋转90°得到ΔABF,连接EF,已知线段EF的长为![]() ,则正方形ABCD的边长为_____
,则正方形ABCD的边长为_____
【答案】5
【解析】
连接BM.先判定△FAE≌△MAB(SAS),即可得到EF=BM.设正方形边长为a,则CM=a-2,Rt△BCM中,利用勾股定理即可得到a的值.
如图,连接BM.
∵△AEM与△ADM关于AM所在的直线对称,∴AE=AD,∠MAD=∠MAE.
∵△ADM按照顺时针方向绕点A旋转90°得到△ABF,∴AF=AM,∠FAB=∠MAD,∴∠FAB=∠MAE,∴∠FAB+∠BAE=∠BAE+∠MAE,∴∠FAE=∠MAB,∴△FAE≌△MAB(SAS),∴EF=BM.
设正方形ABCD的边长为a,则MC=a-2,BC=a.
在Rt△BCM中,∵![]() ,∴
,∴![]() ,解得:a=5或a=-3(舍去),∴正方形的边长为5.
,解得:a=5或a=-3(舍去),∴正方形的边长为5.
故答案为:5.


科目:初中数学 来源: 题型:
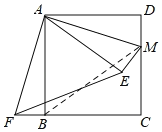
【题目】有一只拉杆式旅行箱如图1,其侧面示意图如图2所示,已知箱体长AB=50 cm,拉杆BC的伸长距离最大时可达35 cm,点A、B、C在同一条直线上,在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面切于点D,在拉杆伸长至最大的情况下,当点B到水平地面MN的距离为38 cm时,点C到水平面的距离CE为59 cm.设AF∥MN,AF交CE于点G(精确到1 cm,参考数据:sin64°≈0.90,cos64°≈0.39,tan64°≈2.1)
(1)求⊙A的半径长;
(2)当人的手自然下垂拉旅行箱时,人感觉较为舒服,某人将手自然下垂在C端拉旅行箱时,CE为80 cm,∠CAF=64°.求此时拉杆BC的伸长距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD的对角线AC、BD相交于点O,AE=CF.
(1)求证:△BOE≌△DOF;
(2)若BD=EF,连接DE、BF,判断四边形EBFD的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数的图象经过点A(2,1)和点B(0,2).
(1)求出函数的关系式;
(2)在平面置角坐标系内画一次函数的图象,回答下列问题:
①y的值随着x的值的增大而 ,它的图象与x轴的交点坐标是 .
②下列点在一次函数图象上的是 ;
(1,![]() ),(﹣2,3),(6,﹣5)
),(﹣2,3),(6,﹣5)
③当x ,时,y>0.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,沿EF将矩形折叠,使A、C重合,AC与EF交于点H.
(1)求证:△ABE≌△AGF;
(2)若AB=6,BC=8,求△ABE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
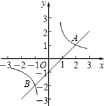
【题目】如图,直线y=x+m与双曲线![]() 相交于A(2,1)、B两点.
相交于A(2,1)、B两点.
(1)求m及k的值;
(2)求出点B的坐标;并直接写出x取何值时,![]() ;
;
(3)P为直线x=![]() 上一点,当△ APB的面积为6时,请直接写出点P的坐标.
上一点,当△ APB的面积为6时,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
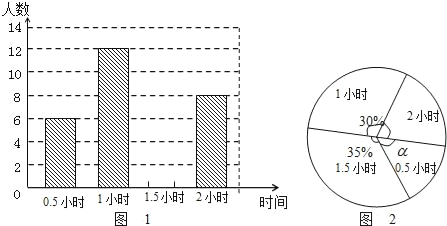
【题目】为了贯彻“减负增效”精神,掌握九年级600名学生每天的自主学习情况,某校学生会随机抽查了九年级的部分学生,并调查他们每天自主学习的时间.根据调查结果,制作了两幅不完整的统计图(图1,图2),请根据统计图中的信息回答下列问题:
(1)本次调查的学生人数是 人;
(2)图2中α是 度,并将图1条形统计图补充完整;
(3)请估算该校九年级学生自主学习时间不少于1.5小时有 人;
(4)老师想从学习效果较好的4位同学(分别记为A、B、C、D,其中A为小亮)随机选择两位进行学习经验交流,用列表法或树状图的方法求出选中小亮A的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.
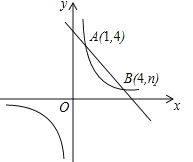
(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.
(1)改扩建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com