
【题目】一次函数的图象经过点A(2,1)和点B(0,2).
(1)求出函数的关系式;
(2)在平面置角坐标系内画一次函数的图象,回答下列问题:
①y的值随着x的值的增大而 ,它的图象与x轴的交点坐标是 .
②下列点在一次函数图象上的是 ;
(1,![]() ),(﹣2,3),(6,﹣5)
),(﹣2,3),(6,﹣5)
③当x ,时,y>0.

【答案】(1)y=﹣![]() x+2;(2)①减小,(4,0);②(1,
x+2;(2)①减小,(4,0);②(1,![]() )和(﹣2,3);③<4.
)和(﹣2,3);③<4.
【解析】
(1)利用待定系数法把A(1,1)和点B(2,﹣1),代入一次函数y=kx+b,可得到一个关于k、b的方程组,再解方程组即可得到k、b的值,然后即可得到一次函数的解析式.
(2)根据两点法画出直线,然后刚好图象解答①②③的问题即可.
(1)设一次函数y=kx+b的图象经过两点A(2,1)和点B(0,2).
∴![]() ,
,
解得: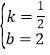 ,
,
∴一次函数解析式为:y=﹣![]() x+2;
x+2;
(2)画一次函数的图象如图所示:
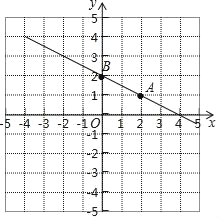
①由图象可知:y的值随着x的值的增大而减小,它的图象与x轴的交点坐标是(4,0);
故答案为:减小,(4,0);
②由图象可知:x=1时,y=![]() ;x=﹣2时,y=3;x=6时,y=﹣1;
;x=﹣2时,y=3;x=6时,y=﹣1;
∴在一次函数图象上的是点(1,![]() )和点(﹣2,3);
)和点(﹣2,3);
故答案为:(1,![]() )和(﹣2,3);
)和(﹣2,3);
③由图象可知:当x<4时,y>0,
故答案为:<4.


科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD相交于点O,点E、F分别是线段AO、BO的中点,若AC+BD=22cm,△OAB的周长是16cm,则EF的长为cm. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣x2+2bx+c与x轴交于点A、B(点A在点B的右侧),且与y轴正半轴交于点C,已知A(2,0) 
(1)当B(﹣4,0)时,求抛物线的解析式;
(2)O为坐标原点,抛物线的顶点为P,当tan∠OAP=3时,求此抛物线的解析式;
(3)O为坐标原点,以A为圆心OA长为半径画⊙A,以C为圆心, ![]() OC长为半径画圆⊙C,当⊙A与⊙C外切时,求此抛物线的解析式.
OC长为半径画圆⊙C,当⊙A与⊙C外切时,求此抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…顶点依次用A1,A2,A3,A4表示,则顶点A2018的坐标是( )

A. (504,﹣504) B. (﹣504,504) C. (505,﹣505) D. (﹣505,505)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,ABCD的顶点B,C在x轴上,A,D两点分别在反比例函数y=﹣ ![]() (x<0)与y=
(x<0)与y= ![]() (x>0)的图象上,则ABCD的面积为 .
(x>0)的图象上,则ABCD的面积为 . 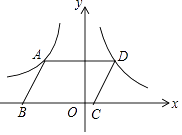
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,我们把,每个小正方形的顶点叫做格点,连接任意两个格点的线段叫网格线段,以网格线段为边组成的图形叫做格点图形,在下列如图所示的正方形网格中,每个小正方形的边长为1. 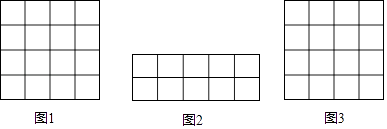
(1)请你在图1中画一个格点图形,且该图形是边长为 ![]() 的菱形;
的菱形;
(2)请你在图2中用网格线段将其切割成若干个三角形和正方形,拼接成一个与其面积相等的正方形,并在图3中画出格点正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以原点O为圆心,3为半径的圆与x轴分别交于A,B两点(点B在点A的右边),P是半径OB上一点,过P且垂直于AB的直线与⊙O分别交于C,D两点(点C在点D的上方),直线AC,DB交于点E.若AC:CE=1:2. 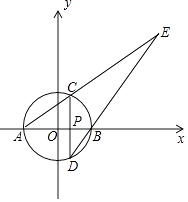
(1)求点P的坐标;
(2)求过点A和点E,且顶点在直线CD上的抛物线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=﹣200x2+400x刻画;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y= ![]() (k>0)刻画(如图所示).
(k>0)刻画(如图所示). 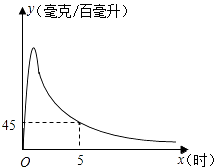
(1)根据上述数学模型计算: ①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当x=5时,y=45,求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com