
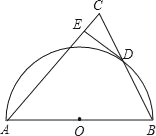
【题目】如图,半圆O的直径为AB,D是半圆上的一个动点(不与点A,B重合),连接BD并延长至点C,使CD=BD,连接AC,过点D作DE⊥AC于点E.
(1)请猜想DE与⊙O的位置关系,并说明理由;
(2)当AB=4,∠BAC=45°时,求DE的长.
【答案】(1)![]() 与
与![]() 相切;(2)
相切;(2)![]()
【解析】
(1)先证明OD为△ABC的中位线得到OD∥AC,再利用DE⊥AC得到OD⊥DE,然后根据切线的判定方法可确定DE为⊙O的切线;
(2)作OF⊥AC于F,如图,证明四边形ODEF为矩形得到OF=DE,再证明△OAF为等腰直角三角形得到OF=![]() ,从而得到DE的长.
,从而得到DE的长.
(1)DE与⊙O相切.理由如下:
连接OD.
∵CD=BD,OA=OB,∴OD为△ABC的中位线,∴OD∥AC.
∵DE⊥AC,∴OD⊥DE,∴DE为⊙O的切线;
(2)作OF⊥AC于F,如图,易得四边形ODEF为矩形,∴OF=DE.
∵∠BAC=45°,∴△OAF为等腰直角三角形,∴OF=![]() OA=
OA=![]() ,∴DE=
,∴DE=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.
(1)求证:ABCD是菱形;
(2)若AB=5,AC=6,求ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的方程x2-2(m+1)x+m2=0.
(1)当m取何值时,方程有两个实数根?
(2)为m选取一个合适的整数,使方程有两个不相等的实数根,并求这两个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想![]() 转化,把未知转化为已知.
转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为x(x2+x-2)=0,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.
(1)问题:方程x3+x2-2x=0的解是x1=0,x2= ,x3= ;
(2)拓展:用“转化”思想求方程![]() 的解;
的解;
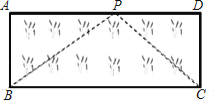
(3)应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
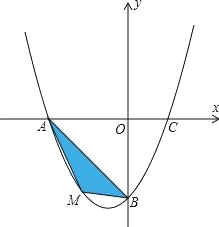
【题目】在平面直角坐标系中,已知抛物线y=![]() +bx﹣4经过A(﹣4,0),C(2,0)两点.
+bx﹣4经过A(﹣4,0),C(2,0)两点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值;
(3)若点P是抛物线上的动点,点Q是直线y=﹣x上的动点,点B是抛物线与y轴交点.判断有几个位置能够使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
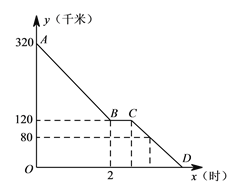
【题目】上周六上午![]() 点,小颖同爸爸妈妈一起从西安出发回安康看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离
点,小颖同爸爸妈妈一起从西安出发回安康看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离![]() (千米)与他们路途所用的时间
(千米)与他们路途所用的时间![]() (时)之间的函数图象,请根据以上信息,解答下列问题:
(时)之间的函数图象,请根据以上信息,解答下列问题:
(1)求直线![]() 所对应的函数关系式;
所对应的函数关系式;
(2)已知小颖一家出服务区后,行驶![]() 分钟时,距姥姥家还有
分钟时,距姥姥家还有![]() 千米,问小颖一家当天几点到达姥姥家?
千米,问小颖一家当天几点到达姥姥家?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年5月31日是世界卫生组织发起的第31个“世界无烟日”.重庆育才中学学生处鼓励学生积极宣传,并设计调查问卷,以更好地宣传吸烟的危害,七年级58班数学兴趣小组第一组的5名同学设计了如下调查问卷,随机调查了部分吸烟人,并将调查结果绘制成统计图.
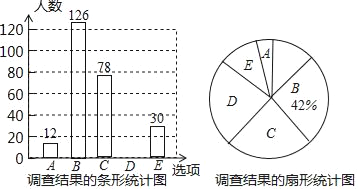
根据以上信息,解答下列问题:
(1)E选项所在扇形的圆心角的度数是 ,并把条形统计图补充完整.
(2)重庆育才中学七年级58班数学兴趣小组第一组的5名同学中有两名男同学们,学校学生处准备从七年级58班数学兴趣小组第一组的5名同学中选取两名同学参加“世界无烟日”活动的总结会,请你用列表法或画树状图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图
(1)指出旋转中心,并求出旋转角的度数.
(2)求出∠BAE的度数和AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
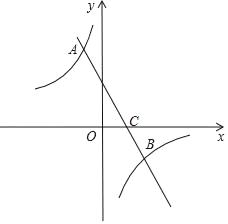
【题目】如图,直线y=kx+b(k≠0)与双曲线y=![]() (m≠0)交于点A(﹣
(m≠0)交于点A(﹣![]() ,2),B(n,﹣1).
,2),B(n,﹣1).
(1)求直线与双曲线的解析式.
(2)点P在x轴上,如果S△ABP=3,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com