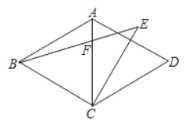
【题目】如图，在菱形
中，
，
，且
，连接
交对角线
于点
，则
______
．
科目：初中数学 来源： 题型：
【题目】如图示，若△ABC内一点P满足∠PAC=∠PBA=∠PCB，则点P为△ABC的布洛卡点．三角形的布洛卡点是法国数学家和教育家克洛尔于1816年首次发现，但他的发现并未被当时的人们所注意，1875年，布洛卡点被一个数学爱好者法国军官布洛卡重新发现，并用他的名字命名．问题：已知在等腰直角三角形DEF中，∠EDF=90°，若点Q为△DEF的布洛卡点，DQ=1，则EQ+FQ=。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，将一副三角板的直角重合放置，其中∠A＝30°，∠CDE＝45°．
（1）如图1，求∠EFB的度数；
（2）若三角板ACB的位置保持不动，将三角板CDE绕其直角顶点C顺时针方向旋转．
①当旋转至如图2所示位置时，恰好CD∥AB，则∠ECB的度数为 ；
②若将三角板CDE继续绕点C旋转，直至回到图1位置．在这一过程中，是否还会存在△CDE其中一边与AB平行？如果存在，请你画出示意图，并直接写出相应的∠ECB的大小；如果不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD的四个顶点分别在四条平行线 
、 
、 
、 
上，这四条直线中相邻两条之间的距离依次为 
、 
、 
（ ＞0， ＞0， ＞0）．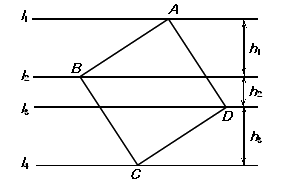
（1）求证： = ；
（2）设正方形ABCD的面积为S，求证：S= 
；
（3）若 
，当 变化时，说明正方形ABCD的面积S随 的变化情况．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】A，B两点在数轴上如图所示，其中O为原点，点A对应的有理数为a，点B对应的有理数为b，且点A距离原点6个单位长度，a．b满足b-|a|=2．
(1)a=______；b=______；
(2)动点P从点A出发，以每秒2个单位长度的速度向右运动，设运动时间为t秒（t＞0）
①当PO=2PB时，求点P的运动时间t：
②当PB=6时，求t的值：
(3)当点P运动到线段OB上时，分别取AP和OB的中点E、F，则
的值是否为一个定值？如果是，求出定值，如果不是，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面是某同学对多项式（x2－4x+2）（x2－4x+6）+4进行因式分解的过程．
解：设x2－4x=y
原式=（y+2）（y+6）+4 （第一步）
=y2+8y+16 （第二步）
=（y+4）2（第三步）
=（x2－4x+4）2（第四步）
回答下列问题：
（1）该同学第二步到第三步运用了因式分解的_______．
A．提取公因式 |
B．平方差公式 |
C．两数和的完全平方公式 |
D．两数差的完全平方公式 |
（2）该同学因式分解的结果是否彻底？________．（填“彻底”或“不彻底”）若不彻底，请直接写出因式分解的最后结果_________ ．
（3）请你模仿以上方法尝试对多项式（x2－2x）（x2－2x+2）+1进行因式分解．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两同学骑自行车从A地沿同一条路到B地，已知乙比甲先出发.他们离出发地的距离s/km和骑行时间t/h之间的函数关系如图所示．根据图象信息，以下说法错误的是（ ）
A.他们都骑了20 km
B.两人在各自出发后半小时内的速度相同
C.甲和乙两人同时到达目的地
D.相遇后，甲的速度大于乙的速度
查看答案和解析>>
科目：初中数学 来源： 题型：
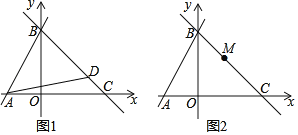
【题目】如图，直线y＝ax+b交x轴于点A，交y轴于点B，且a，b满足a＝
+4，直线y＝kx﹣4k过定点C，点D为直线y＝kx﹣4k上一点，∠DAB＝45°．
（1）a＝ ，b＝ ，C坐标为 ；
（2）如图1，k＝﹣1时，求点D的坐标；
（3）如图2，在（2）的条件下，点M是直线y＝kx﹣4k上一点，连接AM，将AM绕A顺时针旋转90°得AQ，OQ最小值为 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
