
【题目】已知关于 ![]() 的一元二次方程
的一元二次方程 ![]() 有两个实数根
有两个实数根 ![]() 和
和 ![]() .
.
(1)求实数 ![]() 的取值范围;
的取值范围;
(2)当 ![]() 时,求
时,求 ![]() 的值.
的值.
【答案】
(1)解:由题意有 ![]() , 解得
, 解得 ![]() .
.
即实数 ![]() 的取值范围是
的取值范围是 ![]()
(2)解:由 ![]() 得
得 ![]() .
.
若 ![]() ,即
,即 ![]() ,解得
,解得 ![]() .
.
∵ ![]() >
> ![]() ,
, ![]() 不合题意,舍去.
不合题意,舍去.
若 ![]() ,即
,即 ![]()
![]() ,由(1)知
,由(1)知 ![]() .故当
.故当 ![]() 时,
时, ![]() .
.
【解析】(1)利用二次方程有实数根对应的判别式![]() 0,解不等式,可求出m的范围;(2)根据已知可分因式,解得两根之和或差为0,分类计算,求出m.
0,解不等式,可求出m的范围;(2)根据已知可分因式,解得两根之和或差为0,分类计算,求出m.
【考点精析】认真审题,首先需要了解求根公式(根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根),还要掌握根与系数的关系(一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】在锐角△ABC中,∠BAC=60,BD、CE为高,F为BC的中点,连接DE、DF、EF,则结论:①DF=EF;②AD∶AB=AE∶AC;③△DEF是等边三角形;④BE+CD=BC;⑤当∠ABC=45时,BE=![]() DE中,一定正确的有 .
DE中,一定正确的有 . 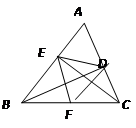
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:已知方程a2![]() 2a
2a![]() 1=0,1
1=0,1![]() 2b
2b![]() b2=0且ab≠1,求
b2=0且ab≠1,求![]() 的值.
的值.
解:由a2![]() 2a
2a![]() 1=0及1
1=0及1![]() 2b
2b![]() b2=0,
b2=0,
可知a≠0,b≠0,
又∵ab≠1,![]() .
.
1![]() 2b
2b![]() b2=0可变形为
b2=0可变形为
![]() ,
,
根据a2![]() 2a
2a![]() 1=0和
1=0和![]() 的特征.
的特征.
![]() 、
、![]() 是方程x2
是方程x2![]() 2x
2x![]() 1=0的两个不相等的实数根,
1=0的两个不相等的实数根,
则![]() ,即
,即![]() .
.
根据阅读材料所提供的方法,完成下面的解答.
已知:3m2![]() 7m
7m![]() 2=0,2n2+7n
2=0,2n2+7n![]() 3=0且mn≠1,求
3=0且mn≠1,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知点C是线段BD上一点,以BC、 DC为一边在BD的同一侧作等边△ABC和等边△ECD,连接AD, BE相交于点F, AC和BE交于点M, AD, CE交于点N,(注:等边三角形的每一个内角都等于60° )
(1) 求证: AD=BE
(2) 线段CM与CN相等吗?请证明你的结论。
(3) 求∠BFD的度数。
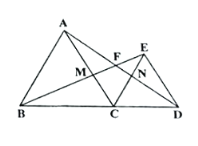
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点A在原点,B、C坐标分别为B(3,0),C(2,2),将△ABC向左平移1个单位后再向下平移2单位,可得到△A′B′C′.
(1)请画出平移后的△A′B′C′的图形;
(2)写出△A′B′C′各个顶点的坐标;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,长方形纸片ABCD的长AD=9cm,宽AB=3cm,将其折叠,使点D与点B重合.
求:(1)折叠后DE的长;(2)以折痕EF为边的正方形面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com