
【题目】解决以下问题:
(1)已知方程组![]() 和方程组
和方程组![]() 有相同的解,求
有相同的解,求![]() 的值;
的值;
(2)已知甲、乙两人解关于![]() 的方程组
的方程组![]() 甲正确解出
甲正确解出![]() 而乙把
而乙把![]() 抄错,结果解得
抄错,结果解得![]() 求
求![]() 的值.
的值.
【答案】(1)a=1,b=2.(2)7
【解析】
(1)先把两个不含a、b的方程重新组合,得到一个只含有x,y的二元一次方程组,利用加减消元法求出x、y的值,然后代入另外两个方程得到关于a、b的二元一次方程组,求解即可.
(2)甲的计算结果正确,可把甲的结果代入原方程,乙的结果是因为c抄错了才计算有误,故可代入第一个方程中,三个方程联立,解三元一次方程组,即可得到a,b,c的值,相加即可.
(1)解:根据题意,方程组重新组合得,![]()
①+②得,5x=15,
解得x=3,
把x=3代入①得,2×3-y=7,
解得y=-1,
∴方程组的解是![]()
代入另两个方程得,![]()
③代入④得,3-(3a-1)=a,
解得a=1,
把a=1代入③得,b=3×1-1=2,
∴a、b的值分别是1,2.
故答案为:a=1,b=2.
(2)甲的计算结果正确,可将![]() 代入
代入![]() 中,
中,
乙仅抄错了c,故可将![]() 代入
代入![]() 中,
中,
联立三个方程组可得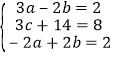
解得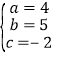
a+b+c=4+5-2=7
故答案为7


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】下列关系中,两个量之间为反比例函数关系的是( )
A.正方形的面积S与边长a的关系
B.正方形的周长L与边长a的关系
C.长方形的长为a,宽为20,其面积S与a的关系
D.长方形的面积为40,长为a,宽为b,a与b的关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市公交公司为应对春运期间的人流高峰,计划购买A、B两种型号的公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车3辆,共需650万元,
(1)试问该公交公司计划购买A型和B型公交车每辆各需多少万元?
(2)若该公司预计在某条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用W不超过1200万元,且确保这10辆公交车在某条线路的年均载客量总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案的总费用W最少?最少总费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/公里计算,耗时费按y元/分钟计算(总费用不足9元按9元计价).小明、小刚两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与打车时间如表:(1)求x,y的值;(2)如果小华也用该打车方式,打车行驶了11公里,用了14分钟,那么小华的打车总费用为多少?
时间(分钟) | 里程数(公里) | 车费(元) | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【发现证明】如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.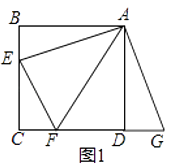
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
(1)【类比引申】如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;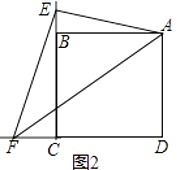
(2)【联想拓展】如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.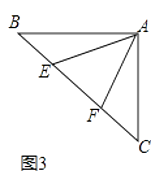
查看答案和解析>>
科目:初中数学 来源: 题型:
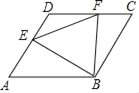
【题目】如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a,△BEF的周长最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com