【题目】如图，已知
的平分线BD和
的平分线CD相交于D，
(1)AB与CD平行吗？请说明理由；
(2)如果
，求
的度数.
科目：初中数学 来源： 题型：
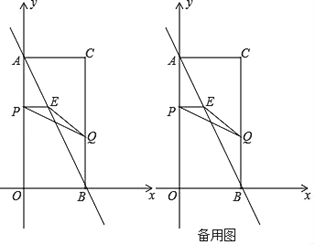
【题目】如图，在平面直角坐标系中，已知矩形AOBC的顶点C的坐标是（2，4），动点P从点A出发，沿线段AO向终点O运动，同时动点Q从点B出发，沿线段BC向终点C运动．点P、Q的运动速度均为每秒1个单位，设运动时间为t秒，过点P作PE⊥AO交AB于点E．
（1）求直线AB的解析式；
（2）在动点P、Q运动的过程中，以B、Q、E为顶点的三角形是直角三角形，直按写出t的值；
（3）设△PEQ的面积为S，求S与时间t的函数关系，并指出自变量t的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料：若
，求m，n的值．
解：
，
．
，
，
，
，
，
，
．
根据你的观察，探究下面的问题：
(1)已知：
，求
的值；
(2)已知：
的三边长a，b，c都是正整数，且满足：
，求的最大边c的值；
(3)已知：
，
，直接写出a的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
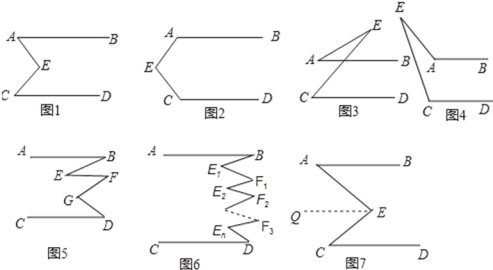
【题目】小红和小明在研究一个数学问题：已知AB∥CD，AB和CD都不经过点E，探索∠E与∠A，∠C的数量关系．
（一）发现：在如图1中，小红和小明都发现：∠AEC=∠A+∠C；
小红是这样证明的：如图7过点E作EQ∥AB．
∴∠AEQ=∠A（ ）
∵EQ∥AB，AB∥CD．
∴EQ∥CD（ ）
∴∠CEQ=∠C
∴∠AEQ+∠CEQ=∠A+∠C 即∠AEC=∠A+∠C．
小明是这样证明的：如图7过点E作EQ∥AB∥CD．
∴∠AEQ=∠A，∠CEQ=∠C
∴∠AEQ+∠CEQ=∠A+∠C即∠AEC=∠A+∠C
请在上面证明过程的横线上，填写依据：两人的证明过程中，完全正确的是 ．
（二）尝试：
（1）在如图2中，若∠A=110°，∠C=130°，则∠E的度数为 ；
（2）在如图3中，若∠A=20°，∠C=50°，则∠E的度数为 ．
（三）探索：
装置如图4中，探索∠E与∠A，∠C的数量关系，并说明理由．
（四）猜想：
（1）如图5，∠B、∠D、∠E、∠F、∠G之间有什么关系？（直接写出结论）
（2）如图6，你可以得到什么结论？（直接写出结论）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知如图等腰
，
，
，
于点D，点P是BA延长线上一点，点O是线段AD上一点，
，下面的结论：
；
是等边三角形；
；
其中正确的是
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AD⊥BC，AE平分∠BAC，∠B=70°，∠C=30°．求：
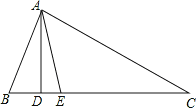
（1）∠BAE的度数；
（2）∠DAE的度数；
（3）探究：小明认为如果条件∠B=70°，∠C=30°改成∠B-∠C=40°，也能得出∠DAE的度数？若能，请你写出求解过程；若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个不透明的袋子里装有8个红球，4个黄球，3个白球，他们除了颜色外都相同，两人做游戏，游戏规则如下：一个人抓住袋子，一个人摸球，若摸出红球，摸球者胜，否则拿袋子的人获胜.
(1)如果你参加游戏，为了尽可能的获胜，你是做摸球的人还是做拿袋子的人?为什么?
(2)你说这个游戏公平吗?如果公平，说明理由：如果不公平，请给出修改建议，使它对双方都是公平的.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
