
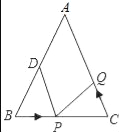
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?
【答案】(1)①△BPD≌△CQP,理由见解析;②![]() cm/s;
cm/s;
(2)经过![]() s点P与点Q第一次在边AB上相遇.
s点P与点Q第一次在边AB上相遇.
【解析】试题分析:(1)①根据时间和速度分别求得两个三角形中的边的长,根据SAS判定两个三角形全等.
②根据全等三角形应满足的条件探求边之间的关系,再根据路程=速度×时间公式,先求得点P运动的时间,再求得点Q的运动速度;
(2)根据题意结合图形分析发现:由于点Q的速度快,且在点P的前边,所以要想第一次相遇,则应该比点P多走等腰三角形的两个腰长.
试题解析:(1)①∵t=1s,
∴BP=CQ=3×1=3cm,
∵AB=10cm,点D为AB的中点,
∴BD=5cm.
又∵PC=BC﹣BP,BC=8cm,
∴PC=8﹣3=5cm,
∴PC=BD.
又∵AB=AC,
∴∠B=∠C,
在△BPD和△CQP中, 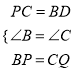 ,
,
∴△BPD≌△CQP(SAS).
②∵vP≠vQ,
∴BP≠CQ,
若△BPD≌△CPQ,∠B=∠C,
则BP=PC=4cm,CQ=BD=5cm,
∴点P,点Q运动的时间![]() ,
,
∴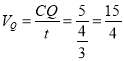 cm/s;
cm/s;
(2)设经过x秒后点P与点Q第一次相遇,
由题意,得![]() x=3x+2×10,
x=3x+2×10,
解得![]() .
.
∴点P共运动了![]() ×3=80cm.
×3=80cm.
△ABC周长为:10+10+8=28cm,
若是运动了三圈即为:28×3=84cm,
∵84﹣80=4cm<AB的长度,
∴点P、点Q在AB边上相遇,
∴经过![]() s点P与点Q第一次在边AB上相遇.
s点P与点Q第一次在边AB上相遇.


科目:初中数学 来源: 题型:
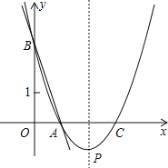
【题目】如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线![]() 经过点A、B,并与x轴交于另一点C,其顶点为P.
经过点A、B,并与x轴交于另一点C,其顶点为P.
(1)求![]() ,
,![]() 的值;
的值;
(2)抛物线的对称轴上有一点Q,使△ABQ是以AB为底边的等腰三角形,求Q点的坐标;
(3)在抛物线及其对称轴上分别取点M、N,使以A,C,M,N为顶点的四边形为正方形,求此正方形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题7分)数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如下:
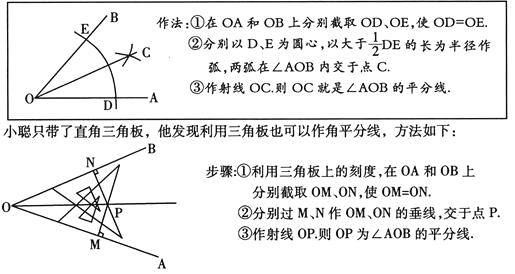
根据以上情境,解决下列问题:
(1)李老师用尺规作角平分线时,用到的三角形全等的判定方法是 .
(2)小聪的作法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 球的三种视图均为同择大小的图形 B. 六棱柱有18条棱,6个侧面,12个顶点
C. 三棱柱的侧面都是三角形 D. 圈柱由两个平面和一个曲面围成
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中,必然事件是( )
A.6月14日晚上能看到月亮
B.早晨的太阳从东方升起
C.打开电视,正在播放新闻
D.任意抛一枚均匀的硬币,正面朝上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)由大小相同的边长为1小立方块搭成的几何体如图,请画出这个几何体的三视图并用阴影表示出来;.

(2)根据三视图:这个组合几何体的表面积为 个平方单位.(包括底面积)
(3)用小立方体搭一几何体,使得它的俯视图和左视图与你在上图方格中所画的图一致,则这样的几何体最少要 个小立方块,最多要 个小立方块.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】让数据说话
你的母亲开了一家服装店,专门卖羽绒服,下面是去年一年各月销售情况表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
销量(件) | 100 | 90 | 50 | 11 | 8 | 6 | 4 | 6 | 5 | 30 | 80 | 110 |
根据表,回答下列问题:
(1)计算去年各季度的销售情况,并用一个适当的统计图表示;
(2)计算去年各季度销售量在全年销售总量中所占的百分比,并用适当统计图表示;
(3)从这些统计图表中,你能得出什么结论为你母亲今后决策能提供什么有用帮助.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com