
【题目】在菱形ABCD中,∠ABC=60°,点P是射线BD上一动点,以AP为边向右侧作等边△APE,点E的位置随着点P的位置变化而变化.

(1)探索发现
如图1,当点E在菱形ABCD内部时,连接CE,BP与CE的数量关系是_______,CE与AD的位置关系是_______.
(2)归纳证明
证明2,当点E在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由.
(3)拓展应用
如图3,当点P在线段BD的延长线上时,连接BE,若AB=5,BE=13,请直接写出线段DP的长.
【答案】(1)BP=CE,CE⊥AD;(2)(1)中的结论仍成立.理由见解析; (3)PD= ![]() .
.
【解析】
(1)由菱形ABCD和∠ABC=60°可证△ABC与△ACD是等边三角形,由等边△APE可得AP=AE,∠PAE=∠BAC=60°,减去公共角∠PAC得∠BAP=∠CAE,根据SAS可证得△BAP≌△CAE,故有BP=CE,∠ABP=∠ACE.由菱形对角线平分一组对角可证∠ABP=30°,故∠ACE=30°即CE平分∠ACD,由AC=CD等腰三角形三线合一可得CE⊥AD.
(2)证明过程同(1).
(3)由AB=5即△ABC为等边三角形可求得BD的长.连接CE,由(2)可求∠BCE=90°,故在Rt△BCE中,由勾股定理可求CE的长.又由(2)可得BP=CE,由DP=BP-BD即求得DP的长.
解:(1) ∵菱形ABCD中,∠ABC=60°
∴AB=BC=CD=AD,∠ADC=∠ABC=60°
∴△ABC、△ACD是等边三角形
∴AB=AC,AC=CD,∠BAC=∠ACD=60°
∵△APE是等边三角形
∴AP=AE,∠PAE=60°
∴∠BAC-∠PAC=∠PAE-∠PAC
即∠BAP=∠CAE
在△BAP与△CAE中
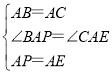
∴△BAP≌△CAE(SAS)
∴BP=CE,∠ABP=∠ACE
∵BD平分∠ABC
∴∠ACE=∠ABP=![]() ∠ABC=30°
∠ABC=30°
∴CE平分∠ACD
∴CE⊥AD
故答案为:BP=CE,CE⊥AD;
(2)(1)中的结论仍成立,证明如下:
设AD与CE交于点O
∵四边形ABCD为菱形,且∠ABC=60°
∴△ABC为等边三角形.
∴AB=AC,∠BAC=60°
∴∠BAP=∠CAE
又∵ΔAPE为等边三角形
∴AP=AE
在△BAP与△CAE中
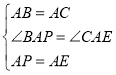
∴△BAP≌ΔCAE(SAS)
∴BP=CE
∴∠ACE=∠ABP=30°
又∵∠CAD=60°
∠A0C=90°
∴AD⊥CE;
(3) 连接CE,设AC与BD相交于点O
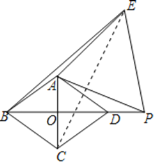
∵AB=5
∴BC=AC=AB=5
∴AO=![]() AC=
AC=![]()
∴BO=![]() =
=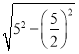 =
=![]()
∴BD=2BO=5![]()
∵∠BCE=∠BCA+∠ACE=90°,BE=13
∴CE=![]() =
=![]() =12
=12
由(2)可知,BP=CE=12
∴DP=BP-BD=12-5![]()
故答案为:(1)BP=CE,CE⊥AD;(2)(1)中的结论仍成立.理由见解析; (3)PD= ![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3cm,BC=6cm.点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
(1)当t为何值时,四边形ABQP是矩形;
(2)当t为何值时,四边形AQCP是菱形;
(3)分别求出(2)中菱形AQCP的周长和面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
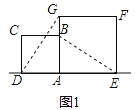
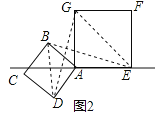
【题目】在数学兴趣小组活动中,小明进行数学探究活动,将边长为![]() 的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线l上,AB与AG在同一直线上.
的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线l上,AB与AG在同一直线上.
(1)图1中,小明发现DG=BE,请你帮他说明理由.
(2)小明将正方形ABCD按如图2那样绕点A旋转一周,旋转到当点C恰好落在直线l上时,请你直接写出此时BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
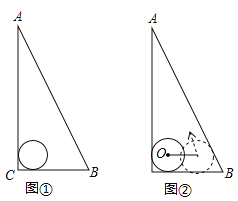
【题目】如图,△ABC是一块直角三角板,且∠C=90°,∠A=30°,现将圆心为点O的圆形纸片放置在三角板内部.
(1)如图①,当圆形纸片与两直角边AC、BC都相切时,试用直尺与圆规作出射线CO;(不写作法与证明,保留作图痕迹)
(2)如图②,将圆形纸片沿着三角板的内部边缘滚动1周,回到起点位置时停止,若BC=9,圆形纸片的半径为2,求圆心O运动的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践与探索
(1)填空: ![]() =______;
=______; ![]() =______;
=______; ![]() =______;
=______; ![]() ______;
______;
(2)观察第(1)题的计算结果回答: ![]() 一定等于
一定等于![]() 吗?你发现其中的规律了吗?请把你观察到的规律归纳出来 。
吗?你发现其中的规律了吗?请把你观察到的规律归纳出来 。
(3)利用你总结的规律计算: ![]() .(2<x<3)
.(2<x<3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个长方体纸盒的平面展开图如图所示,纸盒中相对两个面上的数互为相反数.
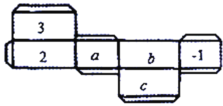
(1)填空:![]() ________,
________,![]() ________,
________,![]() ________.
________.
(2)先化简,再求值:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
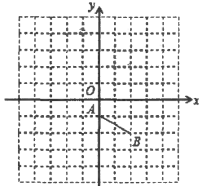
【题目】如图,在正方形网格中,每个小正方形的边长为1个单位长度.平面直角坐标系![]() 的原点
的原点![]() 在格点上,
在格点上,![]() 轴、
轴、![]() 轴都在格线上.线段
轴都在格线上.线段![]() 的两个端点也在格点上.
的两个端点也在格点上.
(1)若将线段![]() 绕点
绕点![]() 逆时针旋转90°得到线段
逆时针旋转90°得到线段![]() ,试在图中画出线段
,试在图中画出线段![]() .
.
(2)若线段![]() 与线段
与线段![]() 关于
关于![]() 轴对称,请画出线段
轴对称,请画出线段![]() .
.
(3)若点![]() 是此平面直角坐标系内的一点,当点
是此平面直角坐标系内的一点,当点![]() 四边围成的四边形为平行四边形 时,请你直接写出点
四边围成的四边形为平行四边形 时,请你直接写出点![]() 的坐标(写出一个即可).
的坐标(写出一个即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
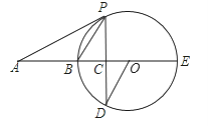
【题目】如图,BE是圆O的直径,A在EB的延长线上,AP为圆O的切线,P为切点,弦PD垂直于BE于点C.
(1)求证:∠AOD=∠APC;
(2)若OC:CB=1:2,AB=6,求圆O的半径及tan∠APB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有个形如六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,依此类推.
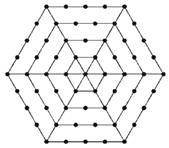
(1)填写下表:
层数 | 1 | 2 | 3 | 4 | 5 | 6 |
该层对应的点数 | 1 | 6 | _____ | 18 | _____ | _____ |
(2)写出第n层所对应的点数为_____;
(3)如果某一层共96个点,那么它是第_____层,此时所有层中共有_____个点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com