
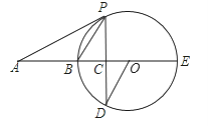
【题目】如图,BE是圆O的直径,A在EB的延长线上,AP为圆O的切线,P为切点,弦PD垂直于BE于点C.
(1)求证:∠AOD=∠APC;
(2)若OC:CB=1:2,AB=6,求圆O的半径及tan∠APB.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)连接OP,可结合已知的等角和等腰三角形、直角三角形的性质进行证明;
(2)根据OC、BC的比例关系,可用未知数表示出OC、BC的表达式,进而可得OP、OB的表达式;在Rt△AOP中,PC⊥OA,根据射影定理得:PC2=PCAC,PC2的表达式可在Rt△OPC中由勾股定理求得,由此求得未知数的知,从而确定PC、CE的长,也就能求出⊙O的半径和∠APB的正切值.
试题解析:(1)连接OP,
∵OP=OD,∴∠OPD=∠D,
∵PD⊥BE,
∴∠OCD=90°,
在Rt△OCD中,∠D+∠AOD=90°,
又∵AP是⊙O的切线,
∴AP⊥OP,
则∠OPD+∠APC=90°,
∴∠AOD=∠APC;
(2)连接PE,
∴∠BPE=90°(直径所对的圆周角是直角),
∵AP是⊙O的切线,
∴∠APB=∠OPE=∠PEA,
∵OC:CB=1:2,
∴设OC=x,则BC=2x,OP=OB=3x,
在Rt△OPC中,OP=3x,OC=x,由勾股定理得:
PC2=OP2﹣OC2=8x2,
在Rt△OPC中,PC⊥OA,由射影定理得:
PC2=OCAC,即8x2=x(2x+6),6x2=6x,
解得x=0(舍去),x=1,
∴OP=OB=3,PC=2![]() ,CE=OC+OE=3+1=4,
,CE=OC+OE=3+1=4,
∴tan∠APB=tan∠PEC=![]() ,
,
∴⊙O的半径为3,∠APB的正切值是![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCD的边BC在x轴的正半轴上,点B在点C的左侧,直线y=kx经过点A(2,2)和点P,且OP=4![]() ,将直线y=kx沿y轴向下平移得到直线y=kx+b,若点P落在矩形ABCD的内部,则b的取值范围是( )
,将直线y=kx沿y轴向下平移得到直线y=kx+b,若点P落在矩形ABCD的内部,则b的取值范围是( )
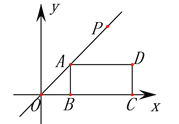
A. 0<b<2 B. -2<b<0 C. -4<b<2 D. -4<b<-2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠ABC=60°,点P是射线BD上一动点,以AP为边向右侧作等边△APE,点E的位置随着点P的位置变化而变化.

(1)探索发现
如图1,当点E在菱形ABCD内部时,连接CE,BP与CE的数量关系是_______,CE与AD的位置关系是_______.
(2)归纳证明
证明2,当点E在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由.
(3)拓展应用
如图3,当点P在线段BD的延长线上时,连接BE,若AB=5,BE=13,请直接写出线段DP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为13cm,弦AB∥CD,AB=24cm,CD=10cm,则AB,CD之间的距离为( )
A. 17cm B. 7cm C. 12cm D. 17cm或7cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个批发店销售同一种苹果,甲批发店的价格为每千克6元.在乙批发店,一次购买数量不超过![]() 时,价格为每千克7元;一次购买数量超过
时,价格为每千克7元;一次购买数量超过![]() 时,其中有
时,其中有![]() 的价格为每千克7元,超过
的价格为每千克7元,超过![]() 部分的价格为每千克5元,设小王在同个批发店一次购买苹果的数量为
部分的价格为每千克5元,设小王在同个批发店一次购买苹果的数量为![]()
![]() .
.
(1)填表:
一次购买苹果的数量(单位: | 20 | 50 | 100 | … |
甲批发店花费(单位:元) | 300 | … | ||
乙批发店花费(单位:元) | 350 | … |
(2)分别用含![]() 的代数式表示甲、乙批发店所花费的钱数.
的代数式表示甲、乙批发店所花费的钱数.
(3)如果小王在同一个批发店一次购买苹果的数量为![]() ,通过计算说明他在甲、乙两个批批发店所花费的钱数少?
,通过计算说明他在甲、乙两个批批发店所花费的钱数少?
查看答案和解析>>
科目:初中数学 来源: 题型:
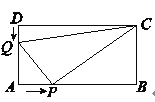
【题目】如图所示,在矩形![]() 中,
中,![]() ,点
,点![]() 沿
沿![]() 边从点
边从点![]() 开始向点
开始向点![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 沿
沿![]() 边从点
边从点![]() 开始向点
开始向点![]() 以
以![]() 的速度移动,如果点
的速度移动,如果点![]() 同时出发,用
同时出发,用![]() 表示移动的时间(
表示移动的时间(![]() ).
).
(1)当![]() 为何值时,
为何值时,![]() 为等腰三角形?
为等腰三角形?
(2)求四边形![]() 的面积,并探索一个与计算结果有关的结论.
的面积,并探索一个与计算结果有关的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A表示数a,点B表示数b,点C表示数c,其中数b是最小的正整数,数a、c满足|a+2|+(c-6)2=0.若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.
![]()
(1)由题意可得:a= ,b= ,c= .
(2)若点A以每秒1个单位长度的速度沿数轴向左运动,点B和点C分别以每秒2个单位长度和3个单位长度的速度沿数轴向右运动,设点A、B、C同时运动,运动时间为t秒.
①当t=2时,分别求AC、AB的长度;
②在点A、B、C同时运动的过程中,3AC-4AB的值是否随着时间t的变化而变化?若变化,说明理由;若不变,求出3AC-4AB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( ).

A. OA=OC,OB=OD B. ∠BAD=∠BCD,AB∥CD
C. AD∥BC,AD=BC D. AB=CD,AO=CO
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com