
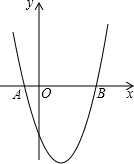
 如图,抛物线y=x2-2x-3与x轴交于A、B两点,直线y=kx-1与抛物线交于P、Q两点,且y轴平分线段PQ,求k的值.
如图,抛物线y=x2-2x-3与x轴交于A、B两点,直线y=kx-1与抛物线交于P、Q两点,且y轴平分线段PQ,求k的值.| x1+x2 |
| 2 |
| 2+k |
| 2 |


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
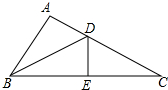 已知在△ABC中,∠A=90°,D,E分别是边BC,AC上的点,且DE⊥BC于D,△ADB≌△EDB≌EDC,则∠C的度数为多少?.DE与DC之间有怎样的数量关系?说明理由.
已知在△ABC中,∠A=90°,D,E分别是边BC,AC上的点,且DE⊥BC于D,△ADB≌△EDB≌EDC,则∠C的度数为多少?.DE与DC之间有怎样的数量关系?说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
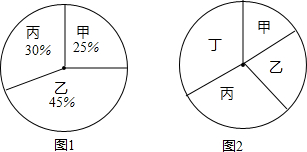 分别求出每个扇形的圆心角的度数.
分别求出每个扇形的圆心角的度数.查看答案和解析>>
科目:初中数学 来源: 题型:
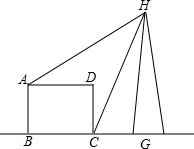 如图所示,形状为长方形的建筑物ABCD的底端BC的长是70cm,高AB=30m,从A,C两点可测得河对面一电视发射塔的顶端H的仰角分别为30°和60°,求塔的高度HG(精确到1m).
如图所示,形状为长方形的建筑物ABCD的底端BC的长是70cm,高AB=30m,从A,C两点可测得河对面一电视发射塔的顶端H的仰角分别为30°和60°,求塔的高度HG(精确到1m).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com