
【题目】如图,已知![]() ,
,![]() ,按如下步骤作图:
,按如下步骤作图:
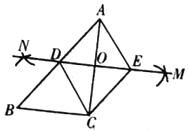
(1)分别以![]() 、
、![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径在
的长为半径在![]() 两边作弧,交于两点
两边作弧,交于两点![]() 、
、![]() ;
;
(2)经过![]() 、
、![]() 作直线,分别交
作直线,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ;
;
(3)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .
.
则下列结论:①![]() 、
、![]() 垂直平分
垂直平分![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④四边形
;④四边形![]() 是菱形;⑤四边形
是菱形;⑤四边形![]() 是菱形.其中一定正确的是______(填序号).
是菱形.其中一定正确的是______(填序号).
【答案】①②④
【解析】
根据题意可知:MN是AC的垂直平分线,①正确;可得AD=CD,AE=CE,然后由CE∥AB,可证得CD∥AE,则四边形ADCE是平行四边形,然后得出![]() ,②正确;继而证得四边形ADCE是菱形,④正确.
,②正确;继而证得四边形ADCE是菱形,④正确.
解:∵分别以A、C为圆心,以大于![]() 的长为半径在AC两边作弧,交于两点M、N,
的长为半径在AC两边作弧,交于两点M、N,
∴MN是AC的垂直平分线,①正确;
∴AD=CD,AE=CE,
∴∠CAD=∠ACD,∠CAE=∠ACE,
∵CE∥AB,
∴∠CAD=∠ACE,
∴∠ACD=∠CAE,
∴CD∥AE,
∴四边形ADCE是平行四边形,
∴![]() ,②正确;
,②正确;
∴四边形ADCE是菱形,④正确;
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]()
∴四边形![]() 是平行四边形,
是平行四边形,
若四边形![]() 是菱形,即
是菱形,即![]() ,
,
若![]() 平分
平分![]() ,即
,即![]() ,
,
题中未限定这两个条件,
∴③⑤不一定正确,
故答案为:①②④.


科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,OD⊥BC于D,∠OCD=40°,则弦BC所对圆周角的度数是( )
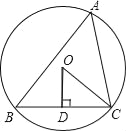
A. 40° B. 50° C. 50°或130° D. 40°或140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:□ABCD的两边AB,AD的长是关于x的方程x2-mx+![]() -
-![]() =0的两个实数根.
=0的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么□ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
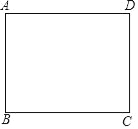
【题目】如图,矩形纸片ABCD,AD=4,AB=3,如果点E在边BC上,将纸片沿AE折叠,使点B落在点F处,联结FC,当△EFC是直角三角形时,那么BE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.
(发现结论)
(1)如图,在□ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连结B′D,发现两个有趣的结论:①△EAC是等腰三角形 ②AC//B′D 请你选择其中一个结论加以证明
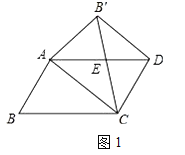
(结论运用)
(2)在□ABCD中,已知:BC=2,∠B=60°,将△ABC沿AC翻折至△AB′C,连结B′D(如上图).若四边形ACDB′是矩形,求AC的长.
(方法拓展)
(3)若 ![]() =k,且以A、C、D、B′为顶点的四边形为正方形,则k的值为 .
=k,且以A、C、D、B′为顶点的四边形为正方形,则k的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,正方形![]() 和正方形
和正方形![]() 共一顶点
共一顶点![]() ,且点
,且点![]() 在
在![]() 上.连接
上.连接![]() 并延长交
并延长交![]() 于点
于点![]() .
.
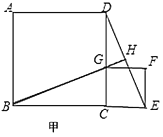
(1)请猜想![]() 与
与![]() 的位置关系和数量关系,并说明理由;
的位置关系和数量关系,并说明理由;
(2)若点![]() 不在
不在![]() 上,其它条件不变,如图乙.
上,其它条件不变,如图乙.![]() 与
与![]() 是否还有上述关系?试说明理由.
是否还有上述关系?试说明理由.
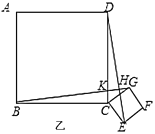
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( )

A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注.某单位计划在室内安装空气净化装置,需购进A、B两种设备.每台B种设备价格比每台A种设备价格多0.7万元,花3万元购买A种设备和花7.2万元购买B种设备的数量相同.
(1)求A种、B种设备每台各多少万元?
(2)根据单位实际情况,需购进A、B两种设备共20台,总费用不高于15万元,求A种设备至少要购买多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com