
【题目】已知等边三角形ABC,AB=12,以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连接GD,
(1)求证:DF与⊙O的位置关系并证明;
(2)求FG的长.
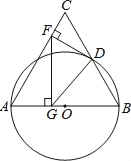
【答案】(1)证明见解析;
(2)FG的长为![]() .
.
【解析】试题分析:(1)连接OD,证∠ODF=90°即可.
(2)利用△ADF是30°的直角三角形可求得AF长,同理可利用△FHC中的60°的三角函数值可求得FG长.
试题解析:(1)连接OD,
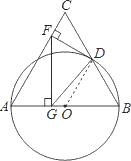
∵以等边三角形ABC的边AB为直径的半圆与BC边交于点D,
∴∠B=∠C=∠ODB=60°,
∴OD∥AC,
∵DF⊥AC,
∴∠CFD=∠ODF=90°,即OD⊥DF,
∵OD是以边AB为直径的半圆的半径,
∴DF是圆O的切线;
(2)∵OB=OD=![]() AB=6,且∠B=60°,
AB=6,且∠B=60°,
∴BD=OB=OD=6,
∴CD=BC﹣BD=AB﹣BD=12﹣6=6,
∵在Rt△CFD中,∠C=60°,
∴∠CDF=30°,
∴CF=![]() CD=
CD=![]() ×6=3,
×6=3,
∴AF=AC﹣CF=12﹣3=9,
∵FG⊥AB,
∴∠FGA=90°,
∵∠FAG=60°,
∴FG=AFsin60°=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点O是△ABC内一点,连接OB、OC,线段AB、OB、OC、AC的中点分别为D、E、F、G.

(1)判断四边形DEFG的形状,并说明理由;
(2)若M为EF的中点,OM=2,∠OBC和∠OCB互余,求线段BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,BE⊥DC交DC的延长线于点E,求证:
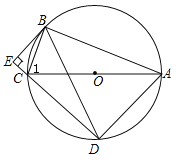
(1)∠1=∠BAD;
(2)BE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,AC为⊙O的切线,OC交⊙O于点D,BD的延长线交AC于点E.
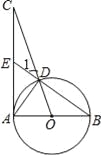
(1)求证:∠1=∠CAD;
(2)若AE=EC=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
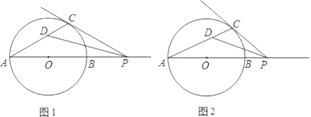
【题目】已知AB为⊙O的直径,P为AB延长线上的任意一点,过点P作⊙O的切线,切点为C,∠APC的平分线PD与AC交于点D.
(1)如图1,若∠CPA恰好等于30°,求∠CDP的度数;
(2)如图2,若点P位于(1)中不同的位置,(1)的结论是否仍然成立?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法不正确的是( )

A.△ABE的面积=△BCE的面积B.∠AFG=∠AGF
C.BH=CHD.∠FAG=2∠ACF
查看答案和解析>>
科目:初中数学 来源: 题型:
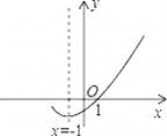
【题目】如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①abc<0;②b>2a;③a+b+c=0④ax2+bx+c=0的两根分别为﹣3和1;⑤8a+c>0.其中正确的命题是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com