
【题目】某段公路经测算发现,匀速行驶的车辆通过该段公路时,所需时间![]() (h)与行驶速度
(h)与行驶速度![]() (km/h)满足反比例函数关系,其图象为如图所示的一段曲线,且端点为A(40,1)和B(m,0.5).
(km/h)满足反比例函数关系,其图象为如图所示的一段曲线,且端点为A(40,1)和B(m,0.5).

(1)求![]() 与
与![]() 的函数关系式及m的值;
的函数关系式及m的值;
(2)若该段公路限速50km/h,求通过该路段需要的最短时间和这段公路的长.
【答案】(1)![]()
(2)0.8h,40km
【解析】(1)设t与y的函数关系式为t=![]() (k≠0)把A的坐标代入解析式,利用待定系数法求得函数解析式,然后爸爸(m,0.5)代入解析式求得m的值;
(k≠0)把A的坐标代入解析式,利用待定系数法求得函数解析式,然后爸爸(m,0.5)代入解析式求得m的值;
(2)求得当y=50时t的值,根据图象即可作出解答.
解:(1)由题意:可设t与y的函数关系式为t=![]() (k≠0),
(k≠0),
∵函数t=![]() 经过点A(40, 1),
经过点A(40, 1),
∴1=![]() ,解得k=40,
,解得k=40,
∴t与y的函数关系式为t=![]() ;
;
把B(m,0.5)代入t=![]() ,
,
得0.5=![]() ,解得m=80;
,解得m=80;
(2)把y=50代入t=![]() ,得t=
,得t=![]() =0.8,
=0.8,
则通过该路段需要的最短时间是0.8小时,这段公路的长为40km.
“点睛”本题考查了反比例函数的实际应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】把下列各数填入表示它所在的集合里.
﹣2,7,﹣1.732,0,3.14,﹣(+5),﹣ ![]() ,﹣(﹣3),2007
,﹣(﹣3),2007
(1)正数集合{ …}
(2)负数集合{ …}
(3)整数集合{ …}
(4)有理数集合{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(三角形顶点是网格线的交点)和△A1B1C1,△ABC与△A1B1C1成中心对称。
(1)画出△ABC和△A1B1C1的对称中心O;
(2)将△A1B1C1,沿直线ED方向向上平移6格,画出△A2B2C2;
(3)将△A2B2C2绕点C2顺时针方向旋转90°,画出△A3B3C3 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的正方形ABCD中,P为对角线AC上的任意一点,分别连接PB、PD,PE⊥PB,交CD与E,
(1)求证:PE=PD;
(2)当E为CD的中点时,求AP的长;
(3)设AP=x(![]() ),四边形BPEC的面积为y,求证:
),四边形BPEC的面积为y,求证: ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两个口袋中,都装有三个相同的小球,分别标有数字1、2、3,小刚、小丽两人进行摸球游戏.游戏规则是:小刚从A袋中随机摸一个球,同时小丽从B袋中随机摸一个球,当两个球上所标数字之和为奇数时小刚赢,否则小丽赢.
(1)这个游戏对双方公平吗?通过列表或画树状图加以说明;
(2)若公平,请你改变本题的游戏规则,使其对小丽有利;若不公平,也请你改变本题的游戏规则,使游戏对双方公平.(无论怎么设计,都请说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
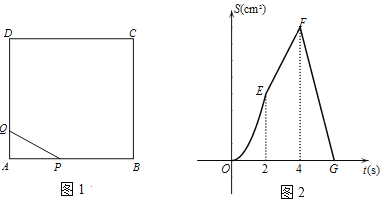
【题目】如图1,四边形![]() 是正方形,动点
是正方形,动点![]() 从点
从点![]() 出发,以
出发,以![]() cm/s的速度沿边
cm/s的速度沿边![]() 、
、![]() 、
、![]() 匀速运动到
匀速运动到![]() 终止;动点
终止;动点![]() 从
从![]() 出发,以
出发,以![]() cm/s的速度沿边
cm/s的速度沿边![]() 匀速运动到
匀速运动到![]() 终止,若
终止,若![]() 、
、![]() 两点同时出发,运动时间为
两点同时出发,运动时间为![]() s,△
s,△![]() 的面积为
的面积为![]() cm2.
cm2. ![]() 与
与![]() 之间函数关系的图像如图
之间函数关系的图像如图![]() 所示.
所示.
(1)求图![]() 中线段
中线段![]() 所表示的函数关系式;
所表示的函数关系式;
(2)当动点![]() 在边
在边![]() 运动的过程中,若以
运动的过程中,若以![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形,求
为顶点的三角形是等腰三角形,求![]() 的值;
的值;
(3)是否存在这样的![]() ,使
,使![]() 将正方形
将正方形![]() 的面积恰好分成
的面积恰好分成![]() 的两部分?若存在,求出这样的
的两部分?若存在,求出这样的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,顶点
,顶点![]() 的横坐标为
的横坐标为![]() .
.

(1)求二次函数的表达式及![]() 的坐标;
的坐标;
(2)若![]() (
(![]() )是
)是![]() 轴上一点,
轴上一点, ![]() ,将点
,将点![]() 绕着点
绕着点![]() 顺时针方向旋转
顺时针方向旋转![]() 得到点
得到点![]() .当点
.当点![]() 恰好在该二次函数的图像上时,求
恰好在该二次函数的图像上时,求![]() 的值;
的值;
(3)在(2)的条件下,连接![]() .若
.若![]() 是该二次函数图像上一点,且
是该二次函数图像上一点,且![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=15,AC=12,BC=9,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF长度的最小值是__.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com