
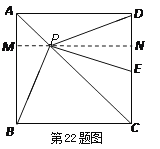
【题目】如图,边长为1的正方形ABCD中,P为对角线AC上的任意一点,分别连接PB、PD,PE⊥PB,交CD与E,
(1)求证:PE=PD;
(2)当E为CD的中点时,求AP的长;
(3)设AP=x(![]() ),四边形BPEC的面积为y,求证:
),四边形BPEC的面积为y,求证: ![]() .
.

【答案】(1)证明见解析;
(2)AP的长为![]() ;
;
(3)证明见解析.
【解析】作PG⊥BC于G,PH⊥CD于H,根据轴对称图形的性质得到PB=PD,PG=PH,证明△BPG≌△EPH,得到PB=PE,等量代换得到答案;
(2)证明∠DPH=∠EPH,根据等腰三角形的性质求出DH,根据勾股定理计算即可;
(3)根据四边形BPEC的面积=正方形PGCH的面积计算.
证明(1)过P作MN∥BC,分别交AB、CD与M、N点;
易证△ABP≌△ADP,∴PD=P
易证△MBP≌△NEP,∴PE=PB
即 PE=PD(2)解:由题意知DN=NE=![]()
又AM=DN
∴AM=![]()
在直角△AMP中,
AP=![]()
(3)证明:当AP=![]() ,则PM=
,则PM=![]() ,
,![]()
设![]() =△PBC的面积,
=△PBC的面积,![]() =△PEC的面积,
=△PEC的面积,
则![]() ,
,![]()
∴![]() =
=![]()
即![]() =
=![]()
“点睛”本题考查的是正方形的性质、全等三角形的判定和性质,掌握正方形的四条边相等、四个角都是90°、一条对角线平分一组对角是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是分,乙队成绩的众数是分;
(2)计算甲、乙队的平均成绩和方差,试说明成绩较为整齐的是哪一队?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某段公路经测算发现,匀速行驶的车辆通过该段公路时,所需时间![]() (h)与行驶速度
(h)与行驶速度![]() (km/h)满足反比例函数关系,其图象为如图所示的一段曲线,且端点为A(40,1)和B(m,0.5).
(km/h)满足反比例函数关系,其图象为如图所示的一段曲线,且端点为A(40,1)和B(m,0.5).

(1)求![]() 与
与![]() 的函数关系式及m的值;
的函数关系式及m的值;
(2)若该段公路限速50km/h,求通过该路段需要的最短时间和这段公路的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某计算装置有一数据输入口A和一运算结果的输出口B,表格中是小明输入的一些数据和这些数据经该装置计算后输出的相应结果,按照这个计算装置的计算规律,若输入的数是10,则输出的数是( )
A | 1 | 2 | 3 | 4 | 5 |
B | 2 | 5 | 10 | 17 | 26 |

A.98
B.99
C.100
D.101
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com