
【题目】如图在平面直角坐标系中抛物线经过A(2,0),B(0,4)两点,将△OAB绕点O逆时针旋转90°得到△OCD,点D在抛物线上.
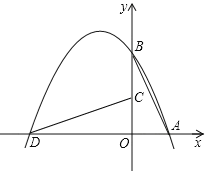
(1)求该抛物线的表达式;
(2)已知点M在y轴上(点M不与点B重合),连接AM,若△AOM与△AOB相似,试求点M的坐标.
【答案】(1)y=-![]() (x-2)(x+4)或y=-
(x-2)(x+4)或y=-![]() x2-x+4;(2)(0,-4)或(0,1)或(0,-1).
x2-x+4;(2)(0,-4)或(0,1)或(0,-1).
【解析】
(1)根据旋转的性质得到点D的坐标,然后利用待定系数法确定函数解析式;
(2)由于△AOM与△AOB相似且∠AOB=∠AOM=90°.所以应该分两种情况:①若![]() =
=![]() ,即
,即![]() =
=![]() ;②
;②![]() =
=![]() ,即
,即![]() =
=![]() ,通过比例式求得符合条件的m的值即可.
,通过比例式求得符合条件的m的值即可.
(1)由旋转的性质可得:OD=OB=4,则D(-4,0).
由抛物线经过点A(2,0),D(-4,0).可设y=a(x-2)(x+4)(a≠0).
把B(0,4)代入,得4=a(0-2)(0+4).
解得a=-![]() .
.
故该抛物线解析式为y=-![]() (x-2)(x+4)或y=-
(x-2)(x+4)或y=-![]() x2-x+4.
x2-x+4.
(2)由题意知,OA=2,OB=4,
设M(0,m),如图所示,
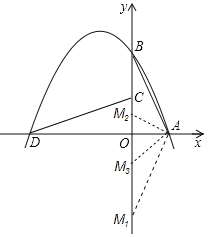
∵△AOM与△AOB相似且∠AOB=∠AOM=90°,
∴分两种情况.
①若![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得m=±4,
∵点M不与点B重合,
∴m=-4符合题意,此时M1(0,-4);
②![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得m=±1,
此时M2(0,1),M2(0,-1),
综上所述,符合条件的点M的坐标是:(0,-4)或(0,1)或(0,-1).


科目:初中数学 来源: 题型:
【题目】如图所示,半圆O的直径AB=4,![]() =
=![]() ,DE⊥AB于E,DF⊥AC于F,连接CD,DB,OD.
,DE⊥AB于E,DF⊥AC于F,连接CD,DB,OD.
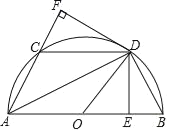
(1)求证:△CDF≌△BDE;
(2)当AD= 时,四边形AODC是菱形;
(3)当AD= 时,四边形AEDF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 和矩形
和矩形![]() 的边
的边![]() 都在直线
都在直线![]() 上,以点
上,以点![]() 为圆心,以24为半径作半圆,分别交直线
为圆心,以24为半径作半圆,分别交直线![]() 于
于![]() 两点.已知:
两点.已知: ![]() ,
,![]() ,矩形自右向左在直线
,矩形自右向左在直线![]() 上平移,当点
上平移,当点![]() 到达点
到达点![]() 时,矩形停止运动.在平移过程中,设矩形对角线
时,矩形停止运动.在平移过程中,设矩形对角线![]() 与半圆
与半圆![]() 的交点为
的交点为![]() (点
(点![]() 为半圆上远离点
为半圆上远离点![]() 的交点).
的交点).
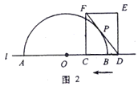
(1)如图2,若![]() 与半圆
与半圆![]() 相切,求
相切,求![]() 的值;
的值;
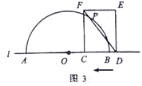
(2)如图3,当![]() 与半圆
与半圆![]() 有两个交点时,求线段
有两个交点时,求线段![]() 的取值范围;
的取值范围;
(3)若线段![]() 的长为20,直接写出此时
的长为20,直接写出此时![]() 的值.
的值.
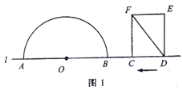
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面直角坐标系中有5个点:A(1,1),B(﹣3,﹣1),C(﹣3,1),D(﹣2.﹣2).

(1)画出△ABC的外接圆⊙P,并指出点D与⊙P相的位置关系;
(2)E点是y轴上的一点,若直线DE与⊙P相切,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20![]() 时,按2元/
时,按2元/![]() 计费;月用水量超过20
计费;月用水量超过20![]() 时,其中的20
时,其中的20![]() 仍按2元/
仍按2元/![]() 收费,超过部分按
收费,超过部分按![]() 元/
元/![]() 计费.设每户家庭用用水量为
计费.设每户家庭用用水量为![]() 时,应交水费
时,应交水费![]() 元.
元.
(1)分别求出![]() 和
和![]() 时
时![]() 与
与![]() 的函数表达式;
的函数表达式;
(2)小明家第二季度交纳水费的情况如下:
月份 | 四月份 | 五月份 | 六月份 |
交费金额 | 30元 | 34元 | 42.6元 |
小明家这个季度共用水多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荣庆公司计划从商店购买同一品牌的台灯和手电筒,已知购买一个台灯比购买一个手电筒多用20元,若用400元购买台灯和用160元购买手电筒,则购买台灯的个数是购买手电筒个数的一半.
(1)求购买该品牌一个台灯、一个手电筒各需要多少元?
(2)经商谈,商店给予荣庆公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠,如果荣庆公司需要手电筒的个数是台灯个数的2倍还多8个,且该公司购买台灯和手电筒的总费用不超过670元,那么荣庆公司最多可购买多少个该品牌台灯?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Q是![]() 上一定点,P是弦AB上一动点,C为AP中点,连接CQ,过点P作
上一定点,P是弦AB上一动点,C为AP中点,连接CQ,过点P作![]() 交
交![]() 于点D,连接AD,CD.
于点D,连接AD,CD.
已知![]() ,设A,P两点间的距离为
,设A,P两点间的距离为![]() ,C,D两点间的距离为
,C,D两点间的距离为![]() .
.
(当点P与点A重合时,令y的值为1.30)
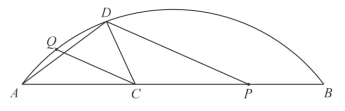
小荣根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探宄.
下面是小荣的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,得到了y与x的几组对应值:

(2)建立平面直角坐标系,描出以补全后的表中各组对应值为坐标的点,画出该函数的图象;

(3)结合函数图象,解决问题:当![]() 时,AP的长度约为__________cm.
时,AP的长度约为__________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小兰用尺规作图作△ABC边AC上的高BH,作法如下:
①分别以点DE为圆心,大于DE的一半长为半径作弧两弧交于F;
②作射线BF,交边AC于点H;
③以B为圆心,BK长为半径作弧,交直线AC于点D和E;
④取一点K使K和B在AC的两侧;
所以BH就是所求作的高.其中顺序正确的作图步骤是( )

A.①②③④B.④③①②C.②④③①D.④③②①
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,A(t,0),B(t+![]() ,0),对于线段AB和点P给出如下定义:当∠APB=90°时,称点P为线段AB的“直角视点”.
,0),对于线段AB和点P给出如下定义:当∠APB=90°时,称点P为线段AB的“直角视点”.
(1)若t=﹣![]() ,在点C(0,
,在点C(0,![]() ),D(﹣1,
),D(﹣1,![]() ),E(
),E(![]() ,
,![]() )中,能够成为线段AB“直角视点”的是 .
)中,能够成为线段AB“直角视点”的是 .
(2)直线MN分别交x轴、y轴于点M、N,点M的坐标是(![]() ,0),∠OMN=30°.
,0),∠OMN=30°.
①线段AB的“直角视点”P在直线MN上,且∠ABP=60°,求点P的坐标.
②在①的条件下,记Q为直线MN上的动点,在点Q的运动过程中,△QAB的周长存在最小值,试求△QAB周长的最小值 .
③若线段AB的所有“直角视点”都在△MON内部,则t的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com