
【题目】如图所示,半圆O的直径AB=4,![]() =
=![]() ,DE⊥AB于E,DF⊥AC于F,连接CD,DB,OD.
,DE⊥AB于E,DF⊥AC于F,连接CD,DB,OD.
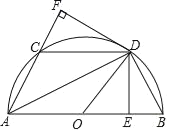
(1)求证:△CDF≌△BDE;
(2)当AD= 时,四边形AODC是菱形;
(3)当AD= 时,四边形AEDF是正方形.
【答案】(1)证明见解析;(2)2![]() ;(3))2
;(3))2![]() .
.
【解析】
(1)根据角平分线的性质,可得DF与DE的关系,根据圆周角定理,可得DC与DB的关系,再根据HL,即可证明;(2)根据菱形的性质,可得OD与CD,OD与BD的关系,根据等边三角形的性质,可得∠DBA的度数,根据三角函数值,即可求解;(3)根据圆周角定理,可得OD⊥AB,根据勾股定理,即可求出AD的长.
(1)证明:∵![]() ,
,
∴CD=BD,∠FAD=∠BAD.
∵DF⊥AC,DE⊥AB,
∴DF=DE,∠BED=∠CFD=90°.
在Rt△CFD和Rt△BED中,![]()
∴△CDF≌△BDE(HL).
(2)四边形AODC是菱形时,
OD=CD=BD=OB,
∴∠DBA=60°,
∴AD=AB·sin∠DBA=4sin60°=2![]() .
.
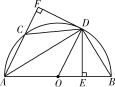
(3)当OD⊥AB,即OD与OE重合时,四边形AEDF是正方形,
由勾股定理得
AD=![]() =2
=2![]() .
.


科目:初中数学 来源: 题型:
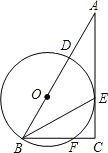
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当今,青少年用电脑手机过多,视力水平下降已引起了全社会的关注,某校为了解八年级1000名学生的视力情况,从中抽查了150名学生的视力情况,通过数据处理,得到如下的频数分布表.解答下列问题:
视力范围分组 | 组中值 | 频数 |
3.95≤x<4.25 | 4.1 | 20 |
4.25≤x<4.55 | 4.4 | 10 |
4.55≤x<4.85 | 4.7 | 30 |
4.85≤x<5.15 | 5.0 | 60 |
5.15≤x<5.45 | 5.3 | 30 |
合计 | 150 |
(1)分别指出参加抽测学生的视力的众数、中位数所在的范围;
(2)若视力为4.85以上(含4.85)为正常,试估计该校八年级学生视力正常的人数约为多少?
(3)根据频数分布表求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数相应组中的权.请你估计该校八年级学生的平均视力是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现如今,通过“微信运动“发布自己每天行走的步数,已成为一种时尚,“健身达人”小华为了了解他的微信朋友圈里大家的“建步走运动“情况,随机抽取了20名好友一天行走的步数,记录如下:
5640 | 6430 | 6320 | 6798 | 7325 | 8430 | 8215 | 7453 | 7446 | 6754 |
7638 | 6834 | 7325 | 6830 | 8648 | 8753 | 9450 | 9865 | 7290 | 7850 |
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
组别 | 步数分组 | 频数 |
A | 5500≤x<6500 | 2 |
B | 6500≤x<7500 | 10 |
C | 7500≤x | m |
D | 8500≤x<9500 | 2 |
E | 9500≤x<10500 | n |
请根据以上信息解答下列问题:
(1)填空:m= ,n= .
(2)补全频数分布直方图.
(3)根据以上统计结果,第二天小华随机查看一名好友行走的步数,试估计该好友的步数不低于7500步(含7500步)的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
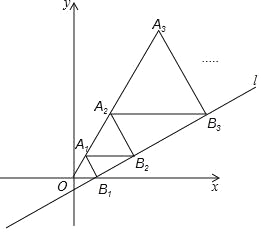
【题目】如图,在平面直角坐标系中,直线l:y=![]() x﹣
x﹣![]() 与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是 .
与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
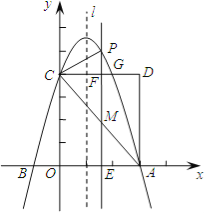
(1)求抛物线的解析式;
(2)抛物线的对称轴l在边OA(不包括O、A两点)上平行移动,分别交x轴于点E,交CD于点F,交AC于点M,交抛物线于点P,若点M的横坐标为m,请用含m的代数式表示PM的长;
(3)在(2)的条件下,连结PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似?若存在,求出此时m的值,并直接判断△PCM的形状;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
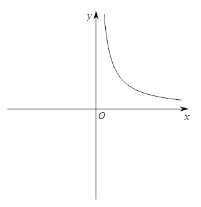
【题目】在研究反比例函数![]() 的图象与性质时,我们对函数解析式进行了深入分析.
的图象与性质时,我们对函数解析式进行了深入分析.
首先,确定自变量![]() 的取值范围是全体非零实数,因此函数图象会被
的取值范围是全体非零实数,因此函数图象会被![]() 轴分成两部分;其次,分析解析式,得到
轴分成两部分;其次,分析解析式,得到![]() 随
随![]() 的变化趋势:当
的变化趋势:当![]() 时,随着
时,随着![]() 值的增大,
值的增大,![]() 的值减小,且逐渐接近于零,随着
的值减小,且逐渐接近于零,随着![]() 值的减小,
值的减小,![]() 的值会越来越大
的值会越来越大![]() ,由此,可以大致画出
,由此,可以大致画出![]() 在
在![]() 时的部分图象,如图1所示:
时的部分图象,如图1所示:
利用同样的方法,我们可以研究函数![]() 的图象与性质. 通过分析解析式画出部分函数图象如图2所示.
的图象与性质. 通过分析解析式画出部分函数图象如图2所示.
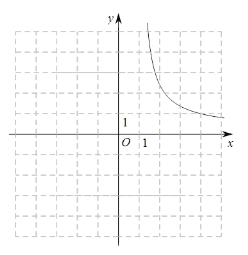
(1)请沿此思路在图2中完善函数图象的草图并标出此函数图象上横坐标为0的点![]() ;(画出网格区域内的部分即可)
;(画出网格区域内的部分即可)
(2)观察图象,写出该函数的一条性质:____________________;
(3)若关于![]() 的方程
的方程![]() 有两个不相等的实数根,结合图象,直接写出实数
有两个不相等的实数根,结合图象,直接写出实数![]() 的取值范围:___________________________.
的取值范围:___________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中抛物线经过A(2,0),B(0,4)两点,将△OAB绕点O逆时针旋转90°得到△OCD,点D在抛物线上.
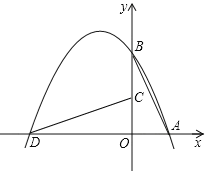
(1)求该抛物线的表达式;
(2)已知点M在y轴上(点M不与点B重合),连接AM,若△AOM与△AOB相似,试求点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com