
【题目】在研究反比例函数![]() 的图象与性质时,我们对函数解析式进行了深入分析.
的图象与性质时,我们对函数解析式进行了深入分析.
首先,确定自变量![]() 的取值范围是全体非零实数,因此函数图象会被
的取值范围是全体非零实数,因此函数图象会被![]() 轴分成两部分;其次,分析解析式,得到
轴分成两部分;其次,分析解析式,得到![]() 随
随![]() 的变化趋势:当
的变化趋势:当![]() 时,随着
时,随着![]() 值的增大,
值的增大,![]() 的值减小,且逐渐接近于零,随着
的值减小,且逐渐接近于零,随着![]() 值的减小,
值的减小,![]() 的值会越来越大
的值会越来越大![]() ,由此,可以大致画出
,由此,可以大致画出![]() 在
在![]() 时的部分图象,如图1所示:
时的部分图象,如图1所示:
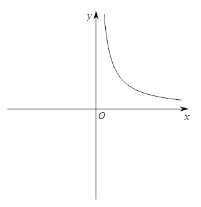
利用同样的方法,我们可以研究函数![]() 的图象与性质. 通过分析解析式画出部分函数图象如图2所示.
的图象与性质. 通过分析解析式画出部分函数图象如图2所示.
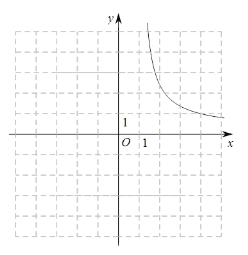
(1)请沿此思路在图2中完善函数图象的草图并标出此函数图象上横坐标为0的点![]() ;(画出网格区域内的部分即可)
;(画出网格区域内的部分即可)
(2)观察图象,写出该函数的一条性质:____________________;
(3)若关于![]() 的方程
的方程![]() 有两个不相等的实数根,结合图象,直接写出实数
有两个不相等的实数根,结合图象,直接写出实数![]() 的取值范围:___________________________.
的取值范围:___________________________.
【答案】(1)详见解析;(2)当![]() 时,
时,![]() 随着
随着![]() 的增大而减小(答案不唯一);(3)
的增大而减小(答案不唯一);(3)![]() .
.
【解析】
(1)首先确定自变量![]() 的取值范围是
的取值范围是![]() 且
且![]() ,因此函数图象会被直线
,因此函数图象会被直线![]() 分成两部分;其次,分析解析式,得到
分成两部分;其次,分析解析式,得到![]() 随
随![]() 的变化趋势:当
的变化趋势:当![]() 时,随着
时,随着![]() 值的增大,
值的增大,![]() 的值减小,且逐渐接近于零;当
的值减小,且逐渐接近于零;当![]() 时,随着
时,随着![]() 值的增大,
值的增大,![]() 的值减小,且逐渐接近于无穷小;当
的值减小,且逐渐接近于无穷小;当![]() 时,
时,![]() ,即点A的坐标为
,即点A的坐标为![]() ,在函数图象上表示出即可.
,在函数图象上表示出即可.
(2)观察分析图象,得出函数的性质,如增减性等.
(3)关于![]() 的方程
的方程![]() 有两个不相等的实数根,则函数
有两个不相等的实数根,则函数![]() 与直线
与直线![]() 有两个不同的交点,根据图象进行分析即可.
有两个不同的交点,根据图象进行分析即可.
(1)自变量![]() 的取值范围是
的取值范围是![]() 且
且![]() ,因此函数图象会被直线
,因此函数图象会被直线![]() 分成两部分;其次,分析解析式,得到
分成两部分;其次,分析解析式,得到![]() 随
随![]() 的变化趋势:当
的变化趋势:当![]() 时,随着
时,随着![]() 值的增大,
值的增大,![]() 的值减小,且逐渐接近于零;当
的值减小,且逐渐接近于零;当![]() 时,随着
时,随着![]() 值的增大,
值的增大,![]() 的值减小,且逐渐接近于无穷小;当
的值减小,且逐渐接近于无穷小;当![]() 时,
时,![]() ,即点A的坐标为
,即点A的坐标为![]() ,.
,.
如图所示:
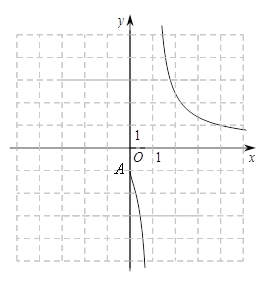
(2)当![]() 时,
时,![]() 随着
随着![]() 的增大而减小;(答案不唯一)
的增大而减小;(答案不唯一)
(3)关于![]() 的方程
的方程![]() 有两个不相等的实数根,则函数
有两个不相等的实数根,则函数![]() 与直线
与直线![]() 有两个不同的交点,
有两个不同的交点,
直线![]() 过定点
过定点![]() ,
,
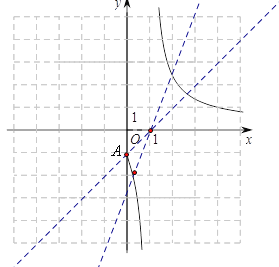
如图当直线![]() 过点A时,函数
过点A时,函数![]() 与直线
与直线![]() 有两个不同的交点,此时
有两个不同的交点,此时![]() 随着
随着![]() 的增大,函数
的增大,函数![]() 与直线
与直线![]() 都有两个不同的交点,
都有两个不同的交点,
故![]() 的取值范围是
的取值范围是![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,点E为矩形ABCD的边AD上一点,点P从点B出发沿BE→ED→DC运动到点C停止,点Q从点B出发沿BC运动到点C停止,它们运动的速度都是1cm/s.若点P、Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2),已知y与t之间的函数图象如图2所示.给出下列结论:①当0<t≤10时,△BPQ是等腰三角形;②S△ABE=48cm2;③14<t<22时,y=110﹣5t;④在运动过程中,使得△ABP是等腰三角形的P点一共有3个;⑤当△BPQ与△BEA相似时,t=14.5.其中正确结论的序号是( )

A. ①④⑤ B. ①②④ C. ①③④ D. ①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,半圆O的直径AB=4,![]() =
=![]() ,DE⊥AB于E,DF⊥AC于F,连接CD,DB,OD.
,DE⊥AB于E,DF⊥AC于F,连接CD,DB,OD.
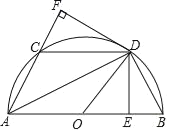
(1)求证:△CDF≌△BDE;
(2)当AD= 时,四边形AODC是菱形;
(3)当AD= 时,四边形AEDF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“过圆上一点作圆的切线”的尺规作图过程.
已知:⊙O和⊙O上一点P.
求作:⊙O的切线MN,使MN经过点P.

作法:如图,
(1)作射线OP;
(2)以点P为圆心,小于OP的长为半径作弧交射线OP于A,B两点;
(3)分别以点A,B为圆心,以大于![]() 长为半径作弧,两弧交于M,N两点;
长为半径作弧,两弧交于M,N两点;
(4)作直线MN.则MN就是所求作的⊙O的切线.
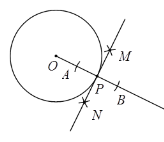
请回答:该尺规作图的依据是____________________________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队承接了60万平方米的绿化工程,由于情况有变,……设原计划每天绿化的面积为![]() 万平方米,列方程为
万平方米,列方程为![]() ,根据方程可知省略的部分是( )
,根据方程可知省略的部分是( )
A. 实际工作时每天的工作效率比原计划提高了![]() 结果提前30天完成了这一任务
结果提前30天完成了这一任务
B. 实际工作时每天的工作效率比原计划提高了![]() ,结果延误30天完成了这一任务
,结果延误30天完成了这一任务
C. 实际工作时每天的工作效率比原计划降低了![]() ,结果延误30天完成了这一任务
,结果延误30天完成了这一任务
D. 实际工作时每天的工作效率比原计划降低了![]() ,结果提前30天完成了这一任务
,结果提前30天完成了这一任务
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 和矩形
和矩形![]() 的边
的边![]() 都在直线
都在直线![]() 上,以点
上,以点![]() 为圆心,以24为半径作半圆,分别交直线
为圆心,以24为半径作半圆,分别交直线![]() 于
于![]() 两点.已知:
两点.已知: ![]() ,
,![]() ,矩形自右向左在直线
,矩形自右向左在直线![]() 上平移,当点
上平移,当点![]() 到达点
到达点![]() 时,矩形停止运动.在平移过程中,设矩形对角线
时,矩形停止运动.在平移过程中,设矩形对角线![]() 与半圆
与半圆![]() 的交点为
的交点为![]() (点
(点![]() 为半圆上远离点
为半圆上远离点![]() 的交点).
的交点).
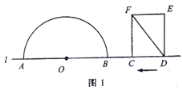
(1)如图2,若![]() 与半圆
与半圆![]() 相切,求
相切,求![]() 的值;
的值;
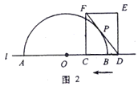
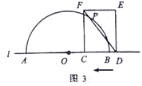
(2)如图3,当![]() 与半圆
与半圆![]() 有两个交点时,求线段
有两个交点时,求线段![]() 的取值范围;
的取值范围;
(3)若线段![]() 的长为20,直接写出此时
的长为20,直接写出此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面直角坐标系中有5个点:A(1,1),B(﹣3,﹣1),C(﹣3,1),D(﹣2.﹣2).

(1)画出△ABC的外接圆⊙P,并指出点D与⊙P相的位置关系;
(2)E点是y轴上的一点,若直线DE与⊙P相切,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小兰用尺规作图作△ABC边AC上的高BH,作法如下:
①分别以点DE为圆心,大于DE的一半长为半径作弧两弧交于F;
②作射线BF,交边AC于点H;
③以B为圆心,BK长为半径作弧,交直线AC于点D和E;
④取一点K使K和B在AC的两侧;
所以BH就是所求作的高.其中顺序正确的作图步骤是( )

A.①②③④B.④③①②C.②④③①D.④③②①
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com