
【题目】在平面直角坐标系xOy中,A(t,0),B(t+![]() ,0),对于线段AB和点P给出如下定义:当∠APB=90°时,称点P为线段AB的“直角视点”.
,0),对于线段AB和点P给出如下定义:当∠APB=90°时,称点P为线段AB的“直角视点”.
(1)若t=﹣![]() ,在点C(0,
,在点C(0,![]() ),D(﹣1,
),D(﹣1,![]() ),E(
),E(![]() ,
,![]() )中,能够成为线段AB“直角视点”的是 .
)中,能够成为线段AB“直角视点”的是 .
(2)直线MN分别交x轴、y轴于点M、N,点M的坐标是(![]() ,0),∠OMN=30°.
,0),∠OMN=30°.
①线段AB的“直角视点”P在直线MN上,且∠ABP=60°,求点P的坐标.
②在①的条件下,记Q为直线MN上的动点,在点Q的运动过程中,△QAB的周长存在最小值,试求△QAB周长的最小值 .
③若线段AB的所有“直角视点”都在△MON内部,则t的取值范围是 .
【答案】(1)C、E;(2)①点P的坐标为 或
或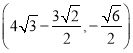 ;②
;②![]() ③
③![]()
【解析】
(1)根据给定的t值找出A、B点的坐标,再利用解三角形的方法讨论C、D、E点是否满足“直角视点”的条件即可得出结论;
(2)①分两种情况:当MN与x轴的夹角∠OMN在x轴上方时和当 MN与x轴的夹角∠OMN在x轴下方时,分别计算点P的坐标即可.
②作A关于MN的对称点A',连接BA'交MN于Q',延长AP交AB于H,H与G重合,连接AA',则AA'⊥MN,AQ'+BQ'=A'B最小,进行计算即可.
③分别计算B点与O重合,点A与M重合时t的值,从而得出线段AB的所有“直角视点”都在△MON内部,则t的取值范围.
解:(1)若![]() 则
则![]()
则![]()
∴![]()
∵点C(0,![]() ),D(﹣1,
),D(﹣1,![]() ),E(
),E(![]() ,
,![]() )
)
由勾股定理得:![]()
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴点C是线段AB的“直角视点”;
同理:
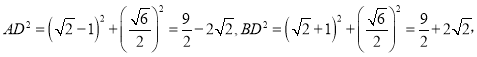
∴![]()
∴![]()
∴点D不是线段AB的“直角视点”;
同理: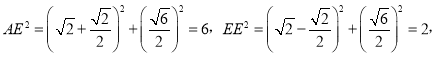
∴AE2+BE2=8=AB2,
∴∠AEB=90°,
∴点E是线段AB的“直角视点”;
故答案为:C、E;
(2)①分两种情况:当MN与x轴的夹角∠OMN在x轴上方时,
∵点P是线段AB的“直角视点”,
∴∠APB=90°,
∴点P在以AB为直径的圆上,
∵∠ABP=60°,
∴∠PAB=30°,
∴![]()
如图1所示:作PG⊥AB于G,

则![]()
∵点M的坐标是![]() ,∠OMN=30°,
,∠OMN=30°,
∴![]()
∴![]()
∴P
当MN与x轴的夹角∠OMN在x轴下方时,同理得:P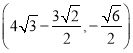
综上所述,点P的坐标为 或
或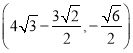 ;
;
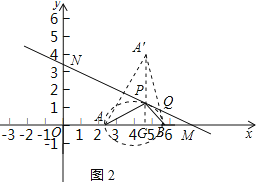
②∵![]() ,若△QAB的周长最小,则AQ+BQ的值最小,
,若△QAB的周长最小,则AQ+BQ的值最小,
作A关于MN的对称点A',连接BA'交MN于Q',延长AP交AB于H,H与G重合,连接AA',
则AA'⊥MN,AQ'+BQ'=A'B最小,
∵∠OMN=30°,
∴∠MAA'=60°,
∵![]()
∴![]()
由勾股定理得: ![]()
∴△QAB最小值为![]()
故答案为:![]()
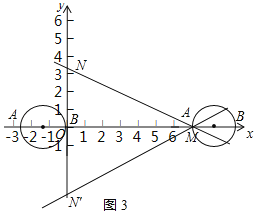
③如图3所示:
当B点与O重合,则![]()
∴![]()
当A与M重合时,![]()
∴若线段AB的所有“直角视点”都在△MON内部,t的取值范围是![]()
故答案为:![]()


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中抛物线经过A(2,0),B(0,4)两点,将△OAB绕点O逆时针旋转90°得到△OCD,点D在抛物线上.
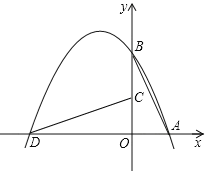
(1)求该抛物线的表达式;
(2)已知点M在y轴上(点M不与点B重合),连接AM,若△AOM与△AOB相似,试求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过![]() 轴正半轴上的任意一点
轴正半轴上的任意一点![]() ,作
,作![]() 轴的平行线,分别与反比例函数
轴的平行线,分别与反比例函数![]() 和
和![]() 的图象交于点
的图象交于点![]() 和点
和点![]() ,点
,点![]() 是
是![]() 轴上一点,连接
轴上一点,连接![]() 、
、![]() ,则
,则![]() 的面积为( )
的面积为( )

A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P,过B点的切线交OP于点C.
(1)求证:∠CBP=∠ADB.
(2)若OA=2,AB=1,求线段BP的长.
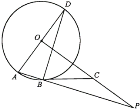
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某种品牌的篮球架实物图与示意图,已知底座BC=0.6米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.5米,篮板顶端F点到篮框D的距离FD=1.4米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离.(精确到0.1米.参考数据:cos75°≈0.3,sin75°≈0.9,.tan75°≈3.7,![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
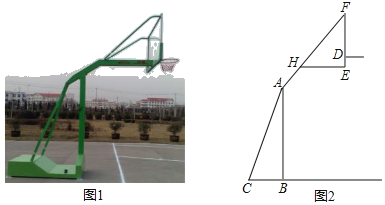
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,AB⊥BC,点E在AB上,∠DEC=90°.
(1)求证:△ADE∽△BEC.
(2)若AD=1,BC=3,AE=2,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器销售商到厂家选购A、B两种型号的液晶电视机,用30000元可购进A型电视10台,B型电视机15台;用30000元可购进A型电视机8台,B型电视机18台.
(1)求A、B两种型号的液晶电视机每台分别多少元?
(2)若该电器销售商销售一台A型液晶电视可获利800元,销售一台B型液晶电视可获利500元,该电器销售商准备用不超过40000元购进A、B两种型号液晶电视机共30台,且这两种液晶电视机全部售出后总获利不低于20400元,问:有几种购买方案?在这几种购买方案中,哪种方案获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于点G,F两点,若M,N分别是DG,CE的中点,则MN的长是______.
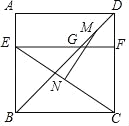
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,在△ABC中,∠ACB=90°,BC=AC,点D在AB上,DE⊥AB交BC于E,点F是AE的中点
(1)写出线段FD与线段FC的关系并证明;
(2)如图2,将△BDE绕点B逆时针旋转α(0°<α<90°),其它条件不变,线段FD与线段FC的关系是否变化,写出你的结论并证明;
(3)将△BDE绕点B逆时针旋转一周,如果BC=4,BE=2![]() ,直接写出线段BF的范围.
,直接写出线段BF的范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com