
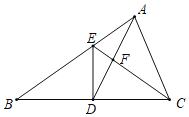
【题目】如图,在△ABC中,AD是BC边上的中线,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD;
(2)过点A作AM⊥BC于点M,求DE:AM的值;
(3)若S△FCD=5,BC=10,求DE的长.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用D是BC边上的中点,DE⊥BC可以得到∠EBC=∠ECB,而由AD=AC可以得到∠ADC=∠ACD,再利用相似三角形的判定定理,就可以证明题目结论;
(2)根据相似三角形的性质和等腰三角形的性质定理,解答即可;
(3)利用相似三角形的性质就可以求出三角形ABC的面积,然后利用面积公式求出AM的值,结合![]() ,即可求解.
,即可求解.
(1)∵D是BC边上的中点,DE⊥BC,
∴BD=DC,∠EDB=∠EDC=90°,
∵DE=DE,
∴△BDE≌△EDC(SAS),
∴∠B=∠DCE,
∵AD=AC,
∴∠ADC=∠ACB,
∴△ABC∽△FCD;
(2)∵AD=AC,AM⊥DC,
∴DM=![]() DC,
DC,
∵BD=DC,
∴![]() ,
,
∵DE⊥BC,AM⊥BC,
∴DE∥AM,
∴![]() .
.
(3)过点A作AM⊥BC,垂足是M,
∵△ABC∽△FCD,BC=2CD,
∴![]() ,
,
∵S△FCD=5,
∴S△ABC=20,
又∵BC=10,
∴AM=4.
∵DE∥AM,
∴![]()
∴![]() ,
,
∴DE=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
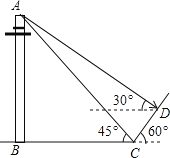
【题目】某校王老师组织九(1)班同学开展数学活动,某天带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A的仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高AB.(结果用根号表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A,B,C,D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).

请根据以上信息回答:
(1)将两幅不完整的图补充完整;
(2)本次参加抽样调查的居民有多少人?
(3)若居民区有8000人,请估计爱吃D粽的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
请根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)请补全频数分布直方图;
(3)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确的个数是( )
①AE=BF;②AE⊥BF;③sin∠BQP=![]() ;④S四边形ECFG=2S△BGE.
;④S四边形ECFG=2S△BGE.
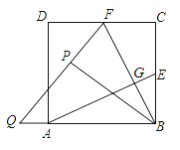
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系xOy中,二次函数y=mx 2 +2mx-4(m≠0)的图象与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,△ABC的面积为12.
(1)求这个二次函数的解析式;
(2)点D的坐标为(-2,1),点P在二次函数的图象上,∠ADP为锐角,且tan∠ADP=2,求出点P的横坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:每个内角都相等的八边形叫做等角八边形.容易知道,等角八边形的内角都等于135°.下面,我们来研究它的一些性质与判定:
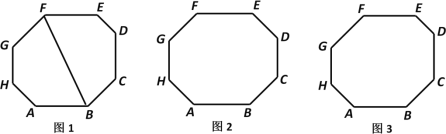
(1)如图1,等角八边形ABCDEFGH中,连结BF.
①请直接写出∠ABF+∠GFB的度数.
②求证:AB∥EF.
③我们把AB与EF称为八边形的一组正对边.由②同理可得:BC与FG,CD与GH,DE与HA这三组正对边也分别平行.请模仿平行四边形性质的学习经验,用一句话概括等角八边形的这一性质.
(2)如图2,等角八边形ABCDEFGH中,如果有AB=EF,BC=FG,则其余两组正对边CD与GH,DE与HA分别相等吗?证明你的结论.
(3)如图3,八边形ABCDEFGH中,若四组正对边分别平行,则显然有∠A=∠E,∠B=∠F,∠C=∠G,∠D=∠H.请探究:该八边形至少需要已知几个内角为135°,才能保证它一定是等角八边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
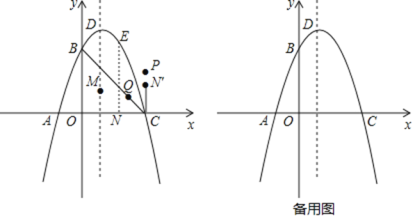
【题目】如图,在平面直角坐标系内,抛物线![]() 与x轴交于点A,C(点A在点C的左侧),与y轴交于点B,顶点为D.点Q为线段BC的三等分点(靠近点C).
与x轴交于点A,C(点A在点C的左侧),与y轴交于点B,顶点为D.点Q为线段BC的三等分点(靠近点C).
(1)点M为抛物线对称轴上一点,点E为对称轴右侧抛物线上的点且位于第一象限,当![]() 的周长最小时,求
的周长最小时,求![]() 面积的最大值;
面积的最大值;
(2)在(1)的条件下,当![]() 的面积最大时,过点E作
的面积最大时,过点E作![]() 轴,垂足为N,将线段CN绕点C顺时针旋转90°得到点N,再将点N向上平移
轴,垂足为N,将线段CN绕点C顺时针旋转90°得到点N,再将点N向上平移![]() 个单位长度.得到点P,点G在抛物线的对称轴上,请问在平面直角坐标系内是否存在一点H,使点D,P,G,H构成菱形.若存在,请直接写出点H的坐标,若不存在,请说明理由.
个单位长度.得到点P,点G在抛物线的对称轴上,请问在平面直角坐标系内是否存在一点H,使点D,P,G,H构成菱形.若存在,请直接写出点H的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com