
【题目】如图,在等边△ABC中,M是边BC延长线上一点,连接AM交△ABC的外接圆于点D,延长BD至N,使得BN=AM,连接CN、MN,
(1)求证:△CMN是等边三角形;
(2)判断CN与⊙O的位置关系,并说明理由;
(3)若AD:AB=3:4,BN=4,求等边△ABC的边长.

【答案】(1)证明见解析;(2)CN是⊙O的切线,理由见解析;(3)等边△ABC的边长是3.
【解析】试题分析:(1)根据全等三角形的判定定理得到△BCN≌△ACM,由全等三角形的性质得到CN=CM,∠BCN=∠ACM,求得∠MCN=∠ACB=60°,即可得到结论;
(2)根据全等三角形的性质得到∠ACO=∠BCO=![]() ACB=30°,根据角的和差得到∠OCN=90°,根据切线的判定定理得到结论;
ACB=30°,根据角的和差得到∠OCN=90°,根据切线的判定定理得到结论;
(3)根据相似三角形的判定和性质即可得到结论.
试题解析:解:(1)在△BCN与△ACM中,∵BC=AC,∠CBN=∠CAM,BN=AM,∴△BCN≌△ACM,∴CN=CM,∠BCN=∠ACM,∴∠BCN﹣∠ACN=∠ACM﹣∠ACN,即∠MCN=∠ACB=60°,∴△CMN是等边三角形;
(2)连接OA.OB.OC,在△BOC与△AOC中,∵OA=OB,AC=BC,OC=OC,∴△BOC≌△AOC,∴∠ACO=∠BCO=![]() ∠ACB=30°,∵∠ACB=∠MCN=60°,∴∠ACN=60°,∴∠OCN=90°,∴OC⊥CN,∴CN是⊙O的切线;
∠ACB=30°,∵∠ACB=∠MCN=60°,∴∠ACN=60°,∴∠OCN=90°,∴OC⊥CN,∴CN是⊙O的切线;
(3)∵∠ADB=∠ACB=60°,∴∠ADB=∠ABC,∵∠BAD=∠MAB,∴△ABD∽△AMB,∴ ![]() ,∵AM=BN=4,∴AB=3,∴等边△ABC的边长是3.
,∵AM=BN=4,∴AB=3,∴等边△ABC的边长是3.



科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 各顶点的坐标分别为
各顶点的坐标分别为![]() ,
,![]() ,
,![]() ,
,![]() ,将四边形
,将四边形![]() 先向上平移3个单位长度,再向左平移5个单位长度,得到四边形
先向上平移3个单位长度,再向左平移5个单位长度,得到四边形![]() .
.
(1)在图中画出四边形![]() ,并写出点
,并写出点![]() 的对应点
的对应点![]() 的坐标;
的坐标;
(2)如果将四边形![]() 看成是由四边形
看成是由四边形![]() 经过一次平移得到的,请指出这一平移的平移方向和平移距离.
经过一次平移得到的,请指出这一平移的平移方向和平移距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C均在坐标轴上,AO=BO=CO=1,过A,O,C作⊙D,E是⊙D上任意一点,连结CE, BE,则![]() 的最大值是( )
的最大值是( )

A. 4 B. 5 C. 6 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,∠BAC=90°,∠BAC和∠ABC的平分线交于点P
(1)如图1,在BC上取一点D,使得DB=AB,连接PD,△ABP与△DBP全等吗?为什么?
(2)在(1)的条件下,若DP=DC,则BC=AB+AP是否成立?请说明理由;
(3)如图2,在AC上取一点E,使得AE=AB,连接PE、PC,若∠ABC=60°,求∠EPC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
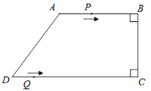
【题目】如图,在四边形ABCD中,AB∥CD,∠ABC=∠BCD=90°,AD=10cm,BC=8cm,CD=16cm.点P从点A出发,以每秒3cm的速度沿折线段AB—BC—CD运动,点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动.已知动点P、Q同时发,设运动时间为t秒(![]() ).
).
(1)求AB的长;
(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;
(3)在点P运动过程中,当![]() 秒的时候,使得△BPD的面积为20cm2.
秒的时候,使得△BPD的面积为20cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某校为了创建书香校园,去年购进一批图书.经了解,科普书的单价比文学书的单价多4元,用12000元购进的科普书与用8000元购进的文学书本数相等.
(1)文学书和科普书的单价各多少钱?
(2)今年文学书和科普书的单价和去年相比保持不变,该校打算用10000元再购进一批文学书和科普书,问购进文学书550本后至多还能购进多少本科普书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系![]() 中,
中,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上靠近点
上靠近点![]() 的三等分点.
的三等分点.

(1)求点![]() 的坐标;
的坐标;
(2)若点![]() 是
是![]() 轴上的一动点,连接
轴上的一动点,连接![]() 、
、![]() ,当
,当![]() 的值最小时,求出
的值最小时,求出![]() 的坐标及
的坐标及![]() 的最小值;
的最小值;
(3)如图2,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,再将
,再将![]() 绕点
绕点![]() 作顺时针方向旋转,旋转角度为
作顺时针方向旋转,旋转角度为![]() ,记旋转中的三角形为
,记旋转中的三角形为![]() ,在旋转过程中,直线
,在旋转过程中,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,当
,当![]() 为等腰三角形时,请直接写出
为等腰三角形时,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 为线段
为线段![]() 上一动点(不与点
上一动点(不与点![]() 、
、![]() 重合),在
重合),在![]() 同侧分别作正三角形
同侧分别作正三角形![]() 和正三角形
和正三角形![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,以下五个结论:①
,以下五个结论:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,⑤
,⑤![]() ,一定成立的是( )
,一定成立的是( )

A.①②③④
B.①②④⑤
C.①②③⑤
D.①③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com