
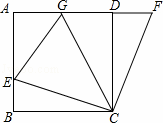
如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且CE=CF.
(1)求证:DF=BE;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
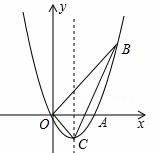
如图,已知抛物线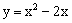 经过点A,B及原点O,顶点为C,直线OB为
经过点A,B及原点O,顶点为C,直线OB为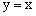 ,点P是抛物线上的动点,过点P作PM⊥x轴,
,点P是抛物线上的动点,过点P作PM⊥x轴, 垂足为M,是否存在点P,使得以P,M,A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
垂足为M,是否存在点P,使得以P,M,A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
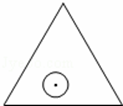
如图, 一个半径为r的圆形纸片在边长为
一个半径为r的圆形纸片在边长为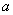
 (
(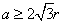
 )的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )
)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )

A.
 B.
B.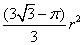
 C.
C.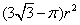
 D.
D.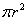

查看答案和解析>>
科目:初中数学 来源: 题型:
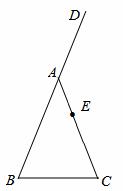
如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E在AC上,且AE=
 CE。
CE。
(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法)。
①作∠DAC的平分线AM。②连接BE并延长交AM于 点F。
点F。
(2)猜想与证明:试猜想AF与BC有怎样的位置关 系和数量关系,并说明理由。
系和数量关系,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
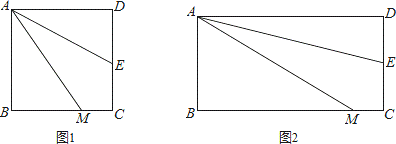
【问题情境】如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请 说明理由.
说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
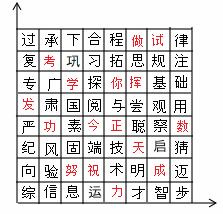
如图是一组密码的一部分.为了保密,许多情况下可采用不同的密码,请你运用所学知识找到破译的“钥匙”。目前,已破译出“正 做数学”的真实意思是“祝你成功”。若“正”所处的位置为(x,y),你找到的密码钥匙是 ,破译的“今天考试”真实意思是 。
做数学”的真实意思是“祝你成功”。若“正”所处的位置为(x,y),你找到的密码钥匙是 ,破译的“今天考试”真实意思是 。
查看答案和解析>>
科目:初中数学 来源: 题型:
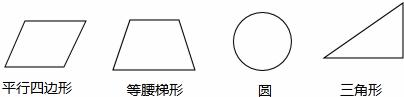
四张质地、大小相同的卡片上,分别画上如下图所示的四个图形,在看不到图形的情况下从中任意抽出一张,则抽出的卡片是中心对称图形的概率为【 】
A. 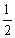 B.
B. 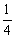 C.
C. 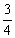 D.1
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com