
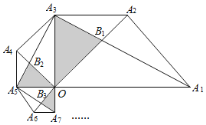
【题目】如图,面积为1的等腰直角△OA1A2,∠OA2A1=90°,且OA2为斜边在△OA1A2外作等腰直角△OA2A3,以OA3为斜边在△OA2A3外作等腰直角△OA3A4,以OA4为斜边在△OA3A4外作等腰直角△OA4A5,…连接A1A3,A3A5,A5A7,…分别与OA2,OA4,OA6,…交于点B1,B2,B3,…按此规律继续下去,记△OB1A3的面积为S1,△OB2A5的面积为S2,△OB3A7的面积为S3,…△OBnA2n+1的面积为Sn,则Sn=__(用含正整数n的式子表示).
【答案】![]()
【解析】
先根据等腰直角三角形的定义求出∠A1OA3=∠OA3A2=90°,得A2A3∥OA1,根据同底等高的两个三角形的面积相等得:![]() ,所以
,所以![]() ,同理得:A4A5∥A3O,同理得:
,同理得:A4A5∥A3O,同理得:![]() ,根据已知的
,根据已知的![]() 1,求对应的直角边和斜边的长:OA2=A1A2
1,求对应的直角边和斜边的长:OA2=A1A2![]() ,A2A3=OA3=1,OA1=2,并利用平行相似证明△A2B1A3∽△OB1A1,列比例式可以求A2B1
,A2A3=OA3=1,OA1=2,并利用平行相似证明△A2B1A3∽△OB1A1,列比例式可以求A2B1![]() ,根据面积公式计算S1
,根据面积公式计算S1![]() ,同理得:S2
,同理得:S2![]() ,从而得出规律.
,从而得出规律.
∵△OA1A2、△OA2A3是等腰直角三角形,∴∠A1OA2=∠A2OA3=45°,∴∠A1OA3=∠OA3A2=90°,∴A2A3∥OA1,∴![]() (同底等高),∴
(同底等高),∴![]() ,∴
,∴![]() ,
,
同理得:A4A5∥A3O,
![]() ,
,
∵![]() 1,∴
1,∴![]() OA2A1A2=1.
OA2A1A2=1.
∵OA2=A1A2,∴OA2=A1A2![]() ,∴A2A3=OA3=1,OA1=2.
,∴A2A3=OA3=1,OA1=2.
∵A2A3∥OA1,∴△A2B1A3∽△OB1A1,∴![]() ,
,
∵A2O![]() ,∴A2B1
,∴A2B1![]() ,∴S1
,∴S1![]() A1A2A2B1
A1A2A2B1![]() ,
,
同理得:OA4=A3A4![]() ,A4A5
,A4A5![]() ,∴△A4A5B2∽△OA3B2,∴
,∴△A4A5B2∽△OA3B2,∴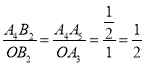 ,∴A4B2
,∴A4B2![]() ,∴S2
,∴S2![]() ,
,
所以得出规律:Sn![]() Sn﹣1
Sn﹣1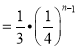 .
.
故答案为: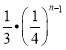 .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,若干个半径为3个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为每秒3个单位长度,点在弧线上的速度为每秒π个单位长度,则2020秒时,点P的坐标是( )
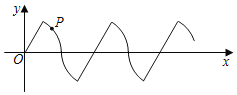
A.(2020,0)B.(3030,0)C.( 3030,![]() )D.(3030,﹣
)D.(3030,﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,![]() ),B(﹣1,m)是一次函数y=kx+b与反比例函数y=
),B(﹣1,m)是一次函数y=kx+b与反比例函数y=![]() 图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
(1)求m的值及一次函数解析式;
(2)P是线段AB上的一点,连接PC、PD,若△PCA和△PDB面积相等,求点P坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,在同一条公路上,匀速行驶,相向而行,到两车相遇时停止.甲车行驶一段时间后,因故停车0.5小时,故障解除后,继续以原速向B地行驶,两车之间的路程y(千米)与出发后所用时间x(小时)之间的函数关系如图所示.

(1)求甲、乙两车行驶的速度V甲、V乙.
(2)求m的值.
(3)若甲车没有故障停车,求可以提前多长时间两车相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC⊥AC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且ADAO=AMAP.
(1)连接OP,证明:△ADM∽△APO;
(2)证明:PD是ΘO的切线;
(3)若AD=24,AM=MC,求![]() 的值.
的值.
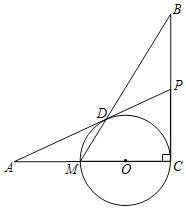
查看答案和解析>>
科目:初中数学 来源: 题型:
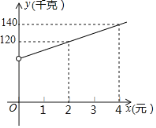
【题目】铁岭市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量y(千克)与每千克降价x(元)(0<x<20)之间满足一次函数关系,其图象如图所示:
(1)求y与x之间的函数关系式;
(2)商贸公司要想获利2090元,则这种干果每千克应降价多少元?
(3)该干果每千克降价多少元时,商贸公司获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a>0)图象的顶点为点D,其图象与x轴的交点A,B的横坐标分别为﹣1和3,给出下列结论:①2a﹣b=0;②a+b+c<0;③3a+c=0;④当a=![]() 时,△ABD是等腰直角三角形.其中,正确的结论有( )
时,△ABD是等腰直角三角形.其中,正确的结论有( )
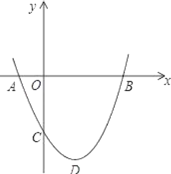
A.①②③B.③④C.②③④D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
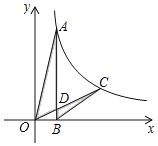
【题目】如图,已知点A,点C在反比例函数y=![]() (k>0,x>0)的图象上,AB⊥x轴于点B,OC交AB于点D,若CD=OD,则△AOD与△BCD的面积比为__.
(k>0,x>0)的图象上,AB⊥x轴于点B,OC交AB于点D,若CD=OD,则△AOD与△BCD的面积比为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
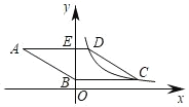
【题目】如图,在平面直角坐标系中,四边形 ABCD是菱形,BC∥x 轴.AD 与 y轴交于点 E,反比例函数 y=![]() (x>0)的图象经过顶点 C、D,已知点 C的横坐标为5,BE=2DE,则 k的值为( )
(x>0)的图象经过顶点 C、D,已知点 C的横坐标为5,BE=2DE,则 k的值为( )
A.![]() B.
B.![]() C.
C.![]() D.5
D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com