Question

12．如图，等边△ABC的边长为2$\sqrt{3}$，以BC边所在直线为x轴，BC边上的高线AO所在的直线为y轴建立平面直角坐标系．
（l）求过A、B、C三点的抛物线的解析式．
（2）如图，设⊙P是△ABC的内切圆，分别切AB、AC于E、F点，圆心P沿y轴运动，设P点坐标为（0，a），则⊙P与直线AB、AC有几种位置关系？并写出相应位置关系时a的取值范围．

Answer 1

分析 （1）由等边三角形的性质求出A、B、C三点坐标，设过A、B、C三点抛物线解析式为y=ax²+bx+c，利用待定系数法即可求得此二次函数的解析式；
（2）由等边三角形的性质得出PA=PB=2OP，得出OA=3OP，再由已知条件求出OP=1，PA=2，得出当a=-1或a=-5时，⊙P与直线AB、AC相切；当-5＜a＜-1时，⊙P与直线AB、AC相交；当a＜-5或a＞-1时，⊙P与直线AB、AC相离即可．

解答 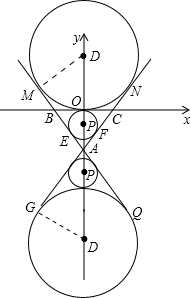解：（1）∵△ABC是等边三角形，AO⊥BC，
∴AC=BC=2$\sqrt{3}$，OB=OC=$\frac{1}{2}$BC=$\sqrt{3}$，
∴OA=$\sqrt{A{C}^{2}-O{C}^{2}}$=3，
∴A（0，-3），B（-$\sqrt{3}$，0），C（$\sqrt{3}$，0），
设过A、B、C三点抛物线解析式为y=ax²+bx+c，
把A、B、C三点坐标代入，得$\left\{\begin{array}{l}{3a+\sqrt{3}b+c=0}&{\;}\\{3a-\sqrt{3}b+c=0}&{\;}\\{c=-3}&{\;}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=1}&{\;}\\{b=0}&{\;}\\{c=-3}&{\;}\end{array}\right.$，
∴所求抛物线解析式为：y=x²-3．
（2）⊙P与直线AB、AC有三种位置关系：相切、相交、相离．理由如下：
连接BP，如图所示：
∵⊙P是△ABC的内切圆，△ABC是等边三角形，
∴∠OBP=30°，PB=PA，
∴PA=PB=2OP，
∴OA=3OP，
∵OA=3，
∴OP=1，PA=2，
∴当a=-1或a=-5时，⊙P与直线AB、AC相切；
当-5＜a＜-1时，⊙P与直线AB、AC相交；
当a＜-5或a＞-1时，⊙P与直线AB、AC相离．

点评 此题是圆的综合题目，考查了待定系数法求二次函数的解析式，等边三角形的性质，直线与圆的位置关系、含30°角的直角三角形的性质等知识；本题综合性强，有一定难度，注意数形结合思想的应用，注意掌握两圆位置关系与圆心距d，两圆半径R，r的数量关系间的关系是解此题的关键．