
【题目】△ABC中,D是BC的中点,点G在AD上(点G不与A重合),过点G的直线交AB于E,交射线AC于点F,设AE=xAB,AF=yAC(x,y≠0).
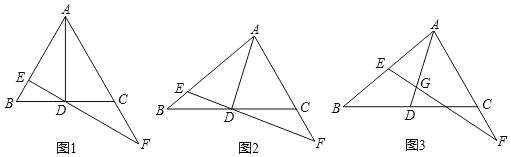
(1)如图1,若△ABC为等边三角形,点G与D重合,∠BDE=30,求证:△AEF∽△DEA;
(2)如图2,若点G与D重合,求证:x+y=2xy;
(3)如图3,若AG=nGD,x=![]() ,y=
,y=![]() ,直接写出n的值.
,直接写出n的值.
【答案】(1)见解析;(2)见解析;(3)n=3
【解析】
(1)先根据等边三角形的性质和中线的性质得到∠BAD=30°,再求得∠F=∠BAD=30°即可证明;
(2)先证明△DEB≌△DHC,得到CH=BE,再证明△FCH∽△FAE,最后运用相似三角形的性质即可证明;
(3)先确定点E是AB的中点,然后根据DE是△ABC的中位线,得出DE=AC,DE//AC可得△DGE∽△AGP,最后运用相似三角形的性质求解即可.
解:(1)∵△ABC为等边三角形,
∴∠BAC=∠B=60°,AB=AC,
∵AD是△ABC的中线,
∴AD平分∠BAC,即∠BAD=![]() ∠BAC=30°,
∠BAC=30°,
∵∠BDE=30°,
∴∠BED=90°,即EF⊥AB
∴∠F=90°-∠EAF=30°
∴∠F=∠BAD
∵∠AED=∠FEA=90°,
∴△AEF∽△DEA;
(2)如图2,过C作CH//AB交EF于H,
∴∠B=∠DCH,∠BED=∠CHD,
∵AD是△ABC的中线
∴BD=CD,
∴△DEB≌△DHC(AAS),
∴CH=BE,
∵CH//AB,
∴△FCH∽△FAE,CF_CH,
∴![]()
∴![]()
∵![]() ,
,![]()
∴![]() ,
,
∴x+y=2xy;
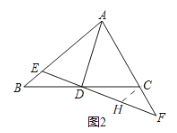
(3)如图3,连接DE
∵y=![]()
∴AF=![]() AC,即AC =
AC,即AC =![]() AF
AF
同理:AE=![]() AB
AB
∴点E是AB的中点。
∵AD是△ABC的中线,即点D是BC的中点,
∴![]()
∵DE//AC.
∴△DGE∽△AGP
∴![]() ,即AG=3DG
,即AG=3DG
∴n=3.



 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,E是AB上的一点,△ADE和△BCE都是等边三角形,点P、Q、M、N分别为AB、BC、CD、DA的中点,则四边形MNPQ是( )
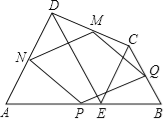
A.等腰梯形B.矩形C.菱形D.正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面上,边长为![]() 的正方形和短边长为
的正方形和短边长为![]() 的矩形几何中心重合,如图①,当正方形和矩形都水平放置时,容易求出重叠面积
的矩形几何中心重合,如图①,当正方形和矩形都水平放置时,容易求出重叠面积![]() .
.
甲、乙、丙三位同学分别给出了两个图形不同的重叠方式;
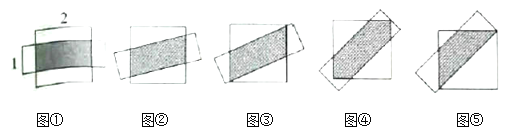
甲:矩形绕着几何中心旋转,从图②到图③的过程中,重叠面积![]() 大小不变.
大小不变.
乙:如图④,矩形绕着几何中心继续旋转,矩形的两条长边与正方形的对角线平行时,此时的重叠面积大于图③的重叠面积.
丙:如图⑤,将图④中的矩形向左上方平移,使矩形的一条长边恰好经过正方形的对角线,此时的重叠面积是![]() 个图形中最小的.
个图形中最小的.
下列说法正确的是( )
A.甲、乙、丙都对B.只有乙对C.只有甲不对D.甲、乙、丙都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于A,B两点(点A在点B左侧)
轴交于A,B两点(点A在点B左侧)
(1)求抛物线的顶点坐标(用含![]() 的代数式表示);
的代数式表示);
(2)求线段AB的长;
(3)抛物线与![]() 轴交于点C(点C不与原点
轴交于点C(点C不与原点![]() 重合),若
重合),若![]() 的面积始终小于
的面积始终小于![]() 的面积,求
的面积,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解下列方程.
①![]() 根为______;
根为______;
②![]() 根为______;
根为______;
③![]() 根为______;
根为______;
(2)根据这类方程特征,写出第n个方程和它的根;
(3)请利用(2)的结论,求关于x的方程![]() (n为正整数)的根.
(n为正整数)的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
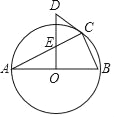
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,∠D=2∠A.
(1)求证:CD是⊙O的切线;
(2)求证:DE=DC;
(3)若OD=5,CD=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
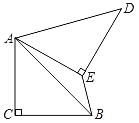
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则∠BED的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数解析式为y=mx2﹣2mx+m﹣![]() ,二次函数与x轴交于A、B两点(B在A右侧),与y轴交于C点,二次函数顶点为M.已知∠OMB=90°.
,二次函数与x轴交于A、B两点(B在A右侧),与y轴交于C点,二次函数顶点为M.已知∠OMB=90°.
①求顶点坐标.
②求二次函数解析式.
③N为线段BM中点,在二次函数的对称轴上是否存在一点P,使得∠PON=60°,若存在求出点P坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.
(1)A、B两种奖品每件各多少元?
(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com