
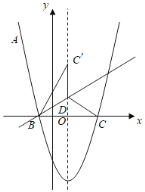
【题目】已知二次函数解析式为y=mx2﹣2mx+m﹣![]() ,二次函数与x轴交于A、B两点(B在A右侧),与y轴交于C点,二次函数顶点为M.已知∠OMB=90°.
,二次函数与x轴交于A、B两点(B在A右侧),与y轴交于C点,二次函数顶点为M.已知∠OMB=90°.
①求顶点坐标.
②求二次函数解析式.
③N为线段BM中点,在二次函数的对称轴上是否存在一点P,使得∠PON=60°,若存在求出点P坐标,若不存在,请说明理由.
【答案】①顶点M(1,﹣![]() );②y
);②y![]() ;③存在,当点P(1,
;③存在,当点P(1,![]() )或(1,﹣3
)或(1,﹣3![]() )时,使得∠PON=60°.
)时,使得∠PON=60°.
【解析】
①先求出对称轴为x=1,代入解析式可求顶点坐标;
②通过证明△MEO∽△BEM,可得![]() ,可求BE=3,可得点B坐标,代入可求解析式;
,可求BE=3,可得点B坐标,代入可求解析式;
③分两种情况讨论,由相似三角形的性质和两点距离公式可求解.
①∵x=﹣![]() =1,
=1,
∴y=m﹣2m+m﹣![]() =﹣
=﹣![]() ,
,
∴顶点M(1,﹣![]() );
);
②如图1,过点M作ME⊥OB于E,
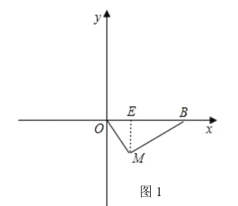
∵顶点M(1,﹣![]() )
)
∴EM=![]() ,OE=1,
,OE=1,
∵∠OMB=90°.
∴∠OME+∠BME=90°,
∵ME⊥OB,
∴∠OME+∠MOE=90°,
∴∠MOE=∠EMB,且∠MEO=∠MEB=90°,
∴△MEO∽△BEM,
∴![]() ,
,
∴BE=3,
∴OB=OE+BE=4,
∴点B(4,0),
∴0=16m﹣8m+m﹣![]() ,
,
∴m=![]() ,
,
∴二次函数解析式为:y![]() ;
;
③如图2,若点P在x轴上方,
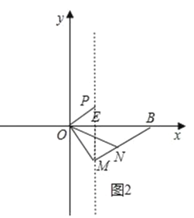
∵顶点M(1,﹣![]() )
)
∴EM=![]() ,OE=1,
,OE=1,
∴tan∠EOM=![]() =
=![]() ,OM=
,OM=![]() =
=![]() =2,
=2,
∴∠EOM=60°,
又∵∠OMB=90°
∴MB=OM![]() tan∠EOM=2
tan∠EOM=2![]() ,
,
∵N为线段BM中点,
∴MN=![]() ,
,
∵∠PON=∠MOB=60°,
∴∠POE=∠OMN,且∠PEO=∠OMN=90°,
∴△OMN∽△OEP,
∴![]() ,
,
∴PE=![]() ,
,
∴点P(1,![]() );
);
如图3,若点P在x轴下方,在OP上截取OF=ON,连接NF,
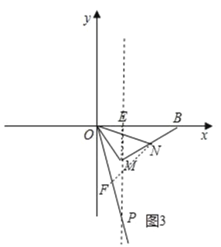
∵OM=2,MN=![]() ,
,
∴ON=![]()
∵ON=OF,∠PON=60°,
∴△ONF是等边三角形,
∴OF=ON=FN=![]() ,
,
∵N为线段BM中点,点B(4,0),点M(1,﹣![]() )
)
∴点N(![]() ,﹣
,﹣![]() )
)
设点F(a,b)
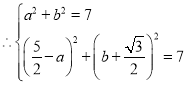
解得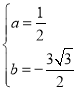
∴点F(![]() ,
,![]() )
)
∴直线OF的解析式为:y=﹣3![]() x,
x,
∴当x=1时,y=﹣3![]() ,
,
∴点P(1,﹣3![]() )
)
综上所述:当点P(1,![]() )或(1,﹣3
)或(1,﹣3![]() )时,使得∠PON=60°.
)时,使得∠PON=60°.


科目:初中数学 来源: 题型:
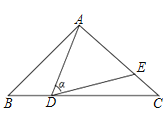
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cos∠α=![]() ,下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或
,下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或![]() ;④0<CE≤6.4.其中正确的结论是_________.(把你认为正确结论的序号都填上)
;④0<CE≤6.4.其中正确的结论是_________.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,D是BC的中点,点G在AD上(点G不与A重合),过点G的直线交AB于E,交射线AC于点F,设AE=xAB,AF=yAC(x,y≠0).
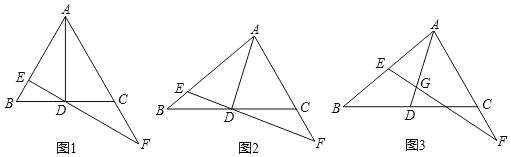
(1)如图1,若△ABC为等边三角形,点G与D重合,∠BDE=30,求证:△AEF∽△DEA;
(2)如图2,若点G与D重合,求证:x+y=2xy;
(3)如图3,若AG=nGD,x=![]() ,y=
,y=![]() ,直接写出n的值.
,直接写出n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某个体地摊经销一批小商品,每件商品的成本为8元.据市场分析,销售单价定为10元时,每天能售出200件;现采用提高商品售价,减少销售量的办法增加利润,若销售单价每涨1元,每天的销售量就减少20件,设销售单价为每件x元,销售量为y件.
(1)写出y与x函数关系式.
(2)若想每天的销售利润恰为640元,同时又要使顾客得到实惠,这种小商品每件售价应定为多少元?
(3)这种小商品每件售价应定为多少元时,每天的销售利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为阻断新冠疫情向校园蔓延,确保师生生命安全和身体健康,教育部通知,2020年春季学期延期开学,利用网上平台,停课不停学”,某校对初三全体学生数学线上学习情况进行调查,随机抽取部分学生的4月月诊断性测试成绩,按由高到低分为A,B,C,D四个等级,根据调查的数据绘制成如下的条形统计图和扇形统计图,请根据图中的信息,解答下列问题:
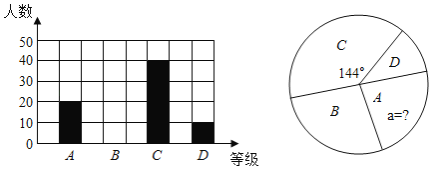
(1)该校共抽查了 名同学的数学测试成绩,扇形统计图中A等级所占的百分比a= ;
(2)补全条形统计图;
(3)若该校初三共有1180名同学,请估计该校初三学生数学测试成绩优秀(测试成绩B级以上为优秀,含B级)约有 名;
(4)该校老师想从两男、两女四位学生中随机选择两位了解平时线上学习情况,请用列表或画树形图的方法求出恰好选中一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面上有且只有4个点,这4个点中有一个独特的性质:连结每两点可得到6条线段,这6条线段有且只有两种长度.我们把这四个点称作准等距点.例如正方形ABCD的四个顶点(如图1),有AB=BC=CD=DA,AC=BD.其实满足这样性质的图形有很多,如图2中A、B、C、O四个点,满足AB=BC=CA,OA=OB=OC;如图3中A、B、C、O四个点,满足OA=OB=OC=BC,AB=AC.
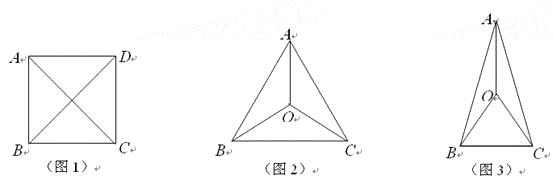
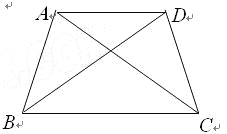
(1)如图,若等腰梯形ABCD的四个顶点是准等距点,且AD∥BC.
①写出相等的线段(不再添加字母);
②求∠BCD的度数.
(2)请再画出一个四边形,使它的四个顶点为准等距点,并写出相等的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
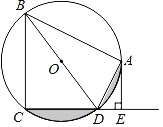
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,AD平分∠BDE.
(1)求证:AE是⊙O的切线;
(2)如果AB=6,AE=3,求:阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() ﹣2x﹣3经过点A(﹣2,a),与x轴相交于B、C两点(B点在C点左侧).
﹣2x﹣3经过点A(﹣2,a),与x轴相交于B、C两点(B点在C点左侧).
(1)求a的值及B、C两点坐标;
(2)点D在抛物线的对称轴上,且位于x轴的上方,将△BCD沿直线BD翻折得到△B![]() D,若点
D,若点![]() 恰好落在抛物线的对称轴上,求点
恰好落在抛物线的对称轴上,求点![]() 和点D的坐标;
和点D的坐标;
(3)设P(m,-3)是该抛物线上一点,点Q为抛物线的顶点,在x轴、y轴分别找点M、N,使四边形MNQP的周长最小,请求出点M、N的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com