
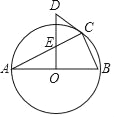
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,∠D=2∠A.
(1)求证:CD是⊙O的切线;
(2)求证:DE=DC;
(3)若OD=5,CD=3,求AC的长.
【答案】(1)见解析;(2)见解析;(3)![]()
![]()
【解析】
(1))连接OC.证∠D=∠COB.由OD⊥AB,得∠COB+∠COD=90°.可证∠D+∠COD=90°.即∠DCO=90°;
(2)由∠DCE+∠ACO=90°,∠AEO+∠A=90°和∠A=∠ACO,∠DEC=∠AEO,可得∠DEC=∠DCE ,即DE=DC.
(3)先求得OC=4,AB=2OC=8, OE=OD-DE=2,再证△AOE∽△ACB,得![]() ,
,
设AC=x,则BC=![]() ,
,
在△ABC中,由AC2+BC2=AB2,求得x=![]() .
.
证明:(1)连接OC.
在⊙O中,OA=OC,
∴∠ACO=∠A,故∠COB=2∠A.
又∵∠D=2∠A,
∴∠D=∠COB.
又∵OD⊥AB,∴∠COB+∠COD=90°.
∴∠D+∠COD=90°.即∠DCO=90°.
即OC⊥DC,又点C在⊙O上,
∴CD是⊙O的切线.

(2)∵∠DCO=90°,∴∠DCE+∠ACO=90°.
又∵OD⊥AB,∴∠AEO+∠A=90°.
又∵∠A=∠ACO,∠DEC=∠AEO,
∴∠DEC=∠DCE
∴DE=DC.
(3)∵∠DCO=90°,OD=5,DC=3,
∴OC=4,
∴AB=2OC=8,又DE=DC,OE=OD-DE=2
在△AOE与△ACB中,
∠A=∠A,∠AOE=∠ACB=90°
∴△AOE∽△ACB,
∴![]() ,
,
设AC=x,则BC=![]()
在△ABC中,AC2+BC2=AB2,求得x=![]()
所以AC的长为![]() .
.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
【题目】西安市的大雁塔又名“慈恩寺塔”,是国家级文物保护单位,玄奘为保存由天竺经丝绸之路带回长安的经卷主持修建了大雁塔,最初五层,后加盖至九层,是西安市的标志性建筑之一,某校社会实践小组为了测量大雁塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,大雁塔的塔尖点B正好在同一直线上,测得EC=4米,将标杆CD向后平移到点G处,这时地面上的点F,标杆的顶端点H,大雁塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得FG=6米,GC=53米,请你根据以上数据,计算大雁塔的高度AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是半圆的直径,
是半圆的直径,![]() 为半圆
为半圆![]() 的圆心,
的圆心,![]() 是弦,取
是弦,取![]() 的中点
的中点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
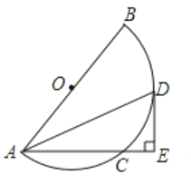
(1)求证:![]() 是半圆
是半圆![]() 的切线;
的切线;
(2)当![]() ,
,![]() 时,求
时,求![]() 的长;
的长;
(3)当![]() 时,直接写出
时,直接写出![]() 面积最大时,点
面积最大时,点![]() 到直径
到直径![]() 的距离.
的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古代算书《算法统宗》中有这样一道题:甲赶群羊逐草茂,乙拽肥羊随其后,戏问甲及一百否?甲云所说无差谬,若得这般一群凑,再添半群小半(注:四分之一的意思)群,得你一只来方凑,玄机奥妙谁参透?大意是说:牧羊人赶着一群羊去寻找草长得茂盛的地方放牧,有一个过路人牵着1只肥羊从后面跟了上来,他对牧羊人说你赶的这群羊大概有100只吧?牧羊人答道:如果这一群羊加上1倍,再加上原来羊群的一半,又加上原来这群羊的四分之一,连你牵着的这只肥羊也算进去,才刚好满100只你知道牧羊人放牧的这群羊一共有多少只吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,D是BC的中点,点G在AD上(点G不与A重合),过点G的直线交AB于E,交射线AC于点F,设AE=xAB,AF=yAC(x,y≠0).
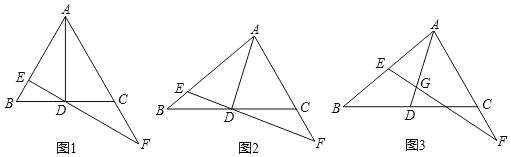
(1)如图1,若△ABC为等边三角形,点G与D重合,∠BDE=30,求证:△AEF∽△DEA;
(2)如图2,若点G与D重合,求证:x+y=2xy;
(3)如图3,若AG=nGD,x=![]() ,y=
,y=![]() ,直接写出n的值.
,直接写出n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与x轴交于A、B两点,与y轴交于C点,连接
与x轴交于A、B两点,与y轴交于C点,连接![]() 、
、![]() ,已知点A、C的坐标为
,已知点A、C的坐标为![]() 、
、![]() .
.
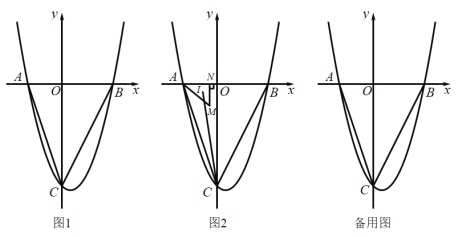
(1)求抛物线的表达式;
(2)点P是线段![]() 下方抛物线上的一动点,如果在x轴上存在点Q,使得以点B、C、P、Q为顶点的四边形为平行四边形,求点Q的坐标;
下方抛物线上的一动点,如果在x轴上存在点Q,使得以点B、C、P、Q为顶点的四边形为平行四边形,求点Q的坐标;
(3)如图2,若点M是![]() 内一动点,且满足
内一动点,且满足![]() ,过点M作
,过点M作![]() ,垂足为N,设
,垂足为N,设![]() 的内心为I,试求
的内心为I,试求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某个体地摊经销一批小商品,每件商品的成本为8元.据市场分析,销售单价定为10元时,每天能售出200件;现采用提高商品售价,减少销售量的办法增加利润,若销售单价每涨1元,每天的销售量就减少20件,设销售单价为每件x元,销售量为y件.
(1)写出y与x函数关系式.
(2)若想每天的销售利润恰为640元,同时又要使顾客得到实惠,这种小商品每件售价应定为多少元?
(3)这种小商品每件售价应定为多少元时,每天的销售利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a,b,c为常数,a<0)经过点(0,2),且关于直线x=﹣1对称,(x1,0)是抛物线与x轴的一个交点,有下列结论,其中结论错误的是( )
A.方程ax2+bx+c=2的一个根是x=﹣2
B.若x1=2,则抛物线与x轴的另一个交点为(﹣4,0)
C.若m=4时,方程ax2+bx+c=m有两个相等的实数根,则a=﹣2
D.若![]() ≤x≤0时,2≤y≤3,则a=
≤x≤0时,2≤y≤3,则a=![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com