
 如图,抛物线$y=-\frac{1}{2}{x^2}+4x-6$与x轴相交于点A、B,与y轴相交于点C,抛物线对称轴与x轴相交于点M,
如图,抛物线$y=-\frac{1}{2}{x^2}+4x-6$与x轴相交于点A、B,与y轴相交于点C,抛物线对称轴与x轴相交于点M,分析 (1)令x=0,可得点C坐标,令y=0,可得点A、B坐标,再结合三角形面积公式,即可得出结论;
(2)找与直线BC平行且过动点P的直线,令此直线与抛物线相切,看切点P是否在x轴上方,如果在,则切点P到直线BC的距离就是所求最大距离,若不在,只需考虑端点A、B到直线BC的距离即可;
(3)过点A作AE⊥BC与点E,并延长AE交直线CP与点D,巧妙利用等腰三角形的三线合一,找出AD、CD的长度,根据两点间的距离公式即可得出结论,不过此处要注意到会产生增根.
解答 解:(1)令y=0,则有-$\frac{1}{2}$x2+4x-6=-$\frac{1}{2}$(x-2)(x-6)=0,
解得:x1=2,x2=6,
即点A(2,0),点B(6,0).
令x=0,则y=-6,
即点C(0,6).
∴AB=4,CO=6.
△ABC的面积S△ABC=$\frac{1}{2}$AB•CO=$\frac{1}{2}$×4×6=12.
(2)设直线BC的解析式为y=kx+b,
∵点B(6,0),点C(0,-6),
∴有$\left\{\begin{array}{l}{0=6k+b}\\{-6=b}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=-6}\end{array}\right.$,
∴直线BC的解析式为y=x-6.
设经过动点P且平行于直线BC的直线解析式为y1=x+a.
将y1=x+a代入抛物线y=-$\frac{1}{2}$x2+4x-6中得:$\frac{1}{2}$x2-3x+6+a=0,
若直线y1=x+a与抛物线相切,则有:
△=(-3)2-4×$\frac{1}{2}$×(6+a)=0,即3+2a=0,
解得:a=-$\frac{3}{2}$.
∴$\frac{1}{2}{x}^{2}$-3x+6-$\frac{3}{2}$=0,即x2-6x+9=0,
解得:x=3,
将x=3代入y1=x-$\frac{3}{2}$,得y1=$\frac{3}{2}$,
∴此时P点坐标为(3,$\frac{3}{2}$)在x轴上方.
∵直线BC的解析式为x-y-6=0,
∴点P到直线BC的距离=$\frac{|3-\frac{3}{2}-6|}{\sqrt{{1}^{2}+(-1)^{2}}}$=$\frac{9\sqrt{2}}{4}$.
故点P到直线BC的距离的最大值为$\frac{9\sqrt{2}}{4}$.
(3)过点A作AE⊥BC与点E,并延长AE交直线CP与点D,如图所示.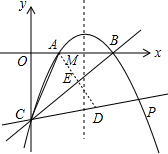
∵点A(2,0),点B(6,0),点O(0,0),点C(0,-6),
∴AB=4,OA=2,OC=6,OB=6.
由勾股定理可知:AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=2$\sqrt{10}$,BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=6$\sqrt{2}$,
∴sin∠OBC=$\frac{OC}{BC}$=$\frac{AE}{AB}$=$\frac{\sqrt{2}}{2}$,AE=2$\sqrt{2}$.
∵∠PCB=∠ACB,且BC⊥AD,
∴CD=CA=2$\sqrt{10}$,DE=AE=2$\sqrt{2}$(等腰三角形三线合一),
∴AD=AE+DE=4$\sqrt{2}$.
设点D坐标为(m,n),
则由两点间的距离公式可知,
$\left\{\begin{array}{l}{(m-0)^{2}+[n-(-6)]^{2}=(2\sqrt{10})^{2}}\\{(m-2)^{2}+(n-0)^{2}=(4\sqrt{2})^{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-\frac{18}{5}}\\{n=-\frac{4}{5}}\end{array}\right.$(舍去)或$\left\{\begin{array}{l}{m=6}\\{n=-4}\end{array}\right.$.
即此时点D的坐标为(6,-4).
设直线CP的解析式为y=k1x-6,将D点坐标代入得:
-4=6k1-6,解得:k1=$\frac{1}{3}$.
∴若点P在抛物线上运动(点P异于点A),当∠PCB=∠BCA时,直线PC的解析式为y=$\frac{1}{3}$x-6.
点评 本题考查了三角形的面积公式、两点间的距离公式、等腰三角形的性质以及点到直线的距离,解题的关键是:(1)牢记三角形面积公式;(2)利用相切法求极值;(3)利用三线合一找到直线CP上除C点外的另一点的坐标.本题属于中档题型,(1)、(2)难度不大,(3)有点难度,由于初中生没有学习过夹角公式,所以只能借助特殊三角形或者三角形全等来解决该类问题.


科目:初中数学 来源: 题型:选择题
| A. | 45cm,65cm | B. | 90cm,110cm | C. | 45cm,55cm | D. | 70cm,90cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5.7112×1012元 | B. | 5.7112×1011元 | C. | 5.7112×1010元 | D. | 5.7112×109元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
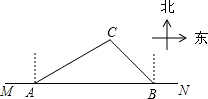 2009年3月21日邵阳市荣获“省卫生城市称号”,在创卫过程中,要在东西方向M、N两地之间修建一条道路,已知:如图,C点周围180米范围内为文物保护区,在MN上点A处测得C在A的北偏东60°方向上,从A向东走500米到达B处,测得C在B的北偏西45°方向上,问MN是否穿过文物保护区?为什么?
2009年3月21日邵阳市荣获“省卫生城市称号”,在创卫过程中,要在东西方向M、N两地之间修建一条道路,已知:如图,C点周围180米范围内为文物保护区,在MN上点A处测得C在A的北偏东60°方向上,从A向东走500米到达B处,测得C在B的北偏西45°方向上,问MN是否穿过文物保护区?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
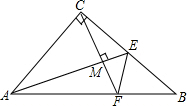 如图,△ABC中,AC=BC,∠ACB=90°.若AE为△ABC的中线,CF⊥AE,垂足为M,交AB于F点,求证:
如图,△ABC中,AC=BC,∠ACB=90°.若AE为△ABC的中线,CF⊥AE,垂足为M,交AB于F点,求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com