练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

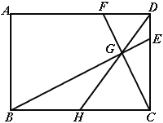
    【题目】如图，在矩形ABCD中，点H为边BC的中点，点G为线段DH上一点，且∠BGC=90°，延长BG交CD于点E，延长CG交AD于点F，当CD=4，DE=1时，则DF的长为（ ）

    A.2B.C.D.

    【答案】A

    【解析】

    延长AD，BE相交于点M，可得△DFG∽△HCG，△DMG∽△HBG，根据相似三角形的性质可得DF=DM，由△MDE∽△CDF可得，进而得出，再根据比例的性质解答即可．

    解：如图，延长AD，BE相交于点M，

    ∵DF∥CH，

    ∴△DFG∽△HCG，

    ∴ ，

    ∵DM∥BH，

    ∴△DMG∽△HBG，

    ∴ ，

    ∵CH=BH， ∴DF=DM，

    又∵矩形

    △MDE∽△CDF，

    ∴

    ∴

    ∴

    ∴DF＝．

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC=5，BC=4,D为边AB上一动点(B点除外)，以CD为一边作正方形CDEF，连接BE，则△BDE面积的最大值为______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某种植户计划将一片荒山改良后种植沃柑，经市场调查得知，当种植沃柑的面积x不超过15亩时，每亩可获得利润y=1900元；超过15亩时，每亩获得利润y（元）与种植面积x（亩）之间的函数关系:y=kx+b，并且当x=20时，y=1800；当x=25时，y=1700．

    （1）请求出y与x的函数关系式，并写出自变量的取值范围；

    （2）设种植户种植x亩沃柑所获得的总利润为w元，由于受条件限制，种植沃柑面积x不超过50亩，求该种植户种植多少亩获得的总利润最大，并求总利润w（元）的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】疫情期间，口罩供不应求．某口罩企业为指导生产，在二月份期间对甲乙丙丁四条生产线日产量进行调研，根据调研数据，绘制出如下两幅不完整的统计图．观察统计图，请解答以下问题：

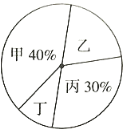
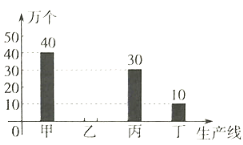
    （1）求二月份该企业口罩单日产量（二月份计天）．

    （2）求乙条生产线单日产量是多少，并补全频数分布直方图．

    （3）为满足市场需求，该公司改进生产技术，使得口罩产量在二月的基础上逐月提高，已知月份口罩产量为万只，若三月份和四月份口罩月产量平均增长率相同，求每月的平均增长率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

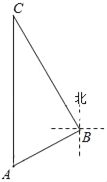
    【题目】我国北斗导航装备的不断更新，极大方便人们的出行．光明中学组织学生利用导航到“金牛山”进行研学活动，到达A地时，发现C地恰好在A地正北方向，且距离A地11.46千米．导航显示路线应沿北偏东60°方同走到B地，再沿北偏西37°方向走一段距离才能到达C地，求B，C两地的距离(精确到1千米)．

    (参考数据sin53°≈0.80，cos53°≈0.60，≈1.73)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某水产养殖户开发一个三角形状的养殖区域，A、B、C三点的位置如图所示．已知∠CAB=105°，∠B=45°，AB=100米．（参考数据：≈1．41，≈1．73，sin20°≈0．34，cos20°≈0．94，tan20°≈0．36，结果保留整数）

    （1）求养殖区域△ABC的面积；

    （2）养殖户计划在边BC上选一点D，修建垂钓栈道AD，测得∠CAD=40°，求垂钓栈道AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

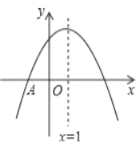
    【题目】如图，抛物线与轴交于点，顶点坐标，则下列结论：

    ①，，；②；③关于的方程有两个不相等的实数根；④．其中结论正确的是（ ）

    A.①B.②③C.②④D.②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】图1是一个闭合时的夹子，图2是该夹子的主视示意图，夹子两边为AC，BD（点A与点B重合），点O是夹子转轴位置，OE⊥AC于点E，OF⊥BD于点F，OE=OF=1cm，AC=BD=6cm， CE=DF， CE:AE=2:3.按图示方式用手指按夹子，夹子两边绕点O转动．

    (1)当E，F两点的距离最大值时，以点A，B，C，D为顶点的四边形的周长是_____ cm．

    (2)当夹子的开口最大（点C与点D重合）时，A，B两点的距离为_____cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

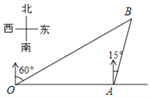
    【题目】如图，港口A在观测站O的正东方向，OA=6km，某船从港口A出发，沿北偏东15°方向航行一段距离后到达B处，此时从观测站O处测得该船位于北偏东60°的方向，则该船航行的距离（即AB的长）为（　　）

    A. 3km B. 3km C. 4km D. （3-3）km

    查看答案和解析>>

    同步练习册答案