
【题目】在平面直角坐标系中,长方形OABC的边OC,OA分别在x轴和y轴上,点B的坐标是(5,3),直线y=2x+b与x轴交于点E,与线段AB交于点F.
(1)用含b的代数式表示点E,F的坐标;
(2)当b为何值时,△OFC是等腰三角形;
(3)当FC平分∠EFB时,求点F的坐标.

【答案】(1)E(﹣![]() ,0);(2)①b=﹣2;②b=﹣5;③b=﹣1.(3)F(
,0);(2)①b=﹣2;②b=﹣5;③b=﹣1.(3)F(![]() ,3).
,3).
【解析】试题分析:(1)根据B、F两点的纵坐标都是3,即可求出点F的坐标,对于直线y=2x+b,令y=0,求出x,可得点E坐标;
(2)分三种情形:①FO=FC.②OF=OC.③CF=OC分别求解即可;
(3)由AB∥OC,CF平分∠EFB,推出∠BFC=∠FCE=∠EFC,推出EF=EC,由此构建方程即可解决问题;
试题解析:解:(1)∵四边形OABC是矩形,∴BF∥OC.∵B(5,3),∴点F的纵坐标为3,∴3=2x+b,∴x=![]() ,∴F(
,∴F(![]() ,3),对于直线y=2x+b,令y=0,得到x=﹣
,3),对于直线y=2x+b,令y=0,得到x=﹣![]() ,∴E(﹣
,∴E(﹣![]() ,0).
,0).
(2)①当FO=FC时,OF=![]() AB=
AB=![]() ,∴
,∴![]() =
=![]() ,∴b=﹣2.
,∴b=﹣2.
②当OF=OC时,AF=![]() =4,∴
=4,∴![]() =4,∴b=﹣5.
=4,∴b=﹣5.
③当CF=OC时,FB=4,AF=1,∴![]() =1,∴b=﹣1.
=1,∴b=﹣1.
(3)如图,连接CF.
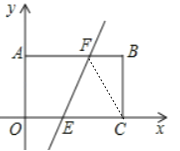
∵AB∥OC,CF平分∠EFB,∴∠BFC=∠FCE=∠EFC,∴EF=EC,∴EF2=EC2.∵F(![]() ,3),E(﹣
,3),E(﹣![]() ,0),∴32+(
,0),∴32+(![]() +
+![]() )2=(5+
)2=(5+![]() )2,∴b=﹣10+3
)2,∴b=﹣10+3![]() 或﹣10﹣3
或﹣10﹣3![]() (舍弃),∴F(
(舍弃),∴F(![]() ,3).
,3).


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】已知四边形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3.
(1)如图1,若P为AB边上一点以PD,PC为边作平行四边形PCQD,请问对角线PQ的长是否存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.
(2)若P为AB边上任意一点,延长PD到E,使DE=PD,再以PE,PC为边作平行四边形PCQE,请问对角线PQ的长是否也存在最小值?如果存在,请直接写出最小值,如果不存在,请说明理由.
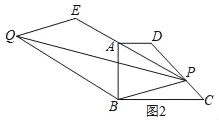
(3)如图2,若P为直线DC上任意一点,延长PA到E,使AE=AP,以PE、PB为边作平行四边形PBQE,请问对角线PQ的长是否存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某巡警车在一条南北大道上巡逻,某天巡警车从岗亭![]() 处出发,规定向北方向为正,当天行驶纪录如下(单位:千米)
处出发,规定向北方向为正,当天行驶纪录如下(单位:千米)
﹣10,﹣9,+7,﹣15,+6,﹣5,+4,﹣2
![]()
(1)最终巡警车是否回到岗亭![]() 处?若没有,在岗亭何方,距岗亭多远?
处?若没有,在岗亭何方,距岗亭多远?
(2)摩托车行驶1千米耗油0.2升,油箱有油10升,够不够?若不够,途中还需补充多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数y=ax2+bx+c(a>0)的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),OB=OC,OC=3OA.
(1)求这个二次函数的表达式;
(2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.
(3)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆半径的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数 | 空间与图形 | 统计与概率 | 综合与实践 | |
学生甲 | 90 | 93 | 89 | 90 |
学生乙 | 94 | 92 | 94 | 86 |
(1)分别计算甲、乙成绩的中位数;
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(n,-2),B(1,4)是一次函数 y=kx+b的图象和反比例函数 ![]() 的图象的两个交点,直线AB与y轴交于点C.
的图象的两个交点,直线AB与y轴交于点C.
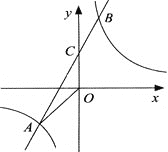
(1)求反比例函数和一次函数的关系式;
(2)求△AOC的面积;
(3)观察图象,直接写出反比例函数值大于一次函数值x取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)已知二次函数y=ax2+bx+1的图象经过点(1,3)和(3,﹣5),求a、b的值;
(2)已知二次函数y=﹣x2+bx+c的图象与x轴的两个交点的横坐标分别为1和2.求这个二次函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017怀化,第10题,4分)如图,A,B两点在反比例函数![]() 的图象上,C,D两点在反比例函数
的图象上,C,D两点在反比例函数![]() 的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则
的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则![]() 的值是( )
的值是( )

A. 6 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大家看过中央电视台“购物街”节目吗?其中有一个游戏环节是大转轮比赛,转轮上平均分布着5、10、15、20一直到100共20个数字.选手依次转动转轮,每个人最多有两次机会.选手转动的数字之和最大不超过100者为胜出;若超过100则成绩无效,称为“爆掉”.
(1)某选手第一次转到了数字5,再转第二次,则他两次数字之和为100的可能性有多大?
(2)现在某选手第一次转到了数字65,若再转第二次了则有可能“爆掉”,请你分析“爆掉”的可能性有多大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com