
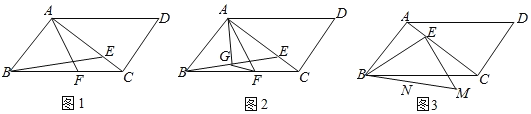
【题目】在ABCD中,AF平分∠BAD交BC于点F,∠BAC=90°,点E是对角线AC上的点,连结BE.
(1)如图1,若AB=AE,BF=3,求BE的长;
(2)如图2,若AB=AE,点G是BE的中点,∠FAG=∠BFG,求证:AB![]() FG;
FG;
(3)如图3,以点E为直角顶点,在BE的右下方作等腰直角△BEM,若点E从点A出发,沿AC运动到点C停止,设在点E运动过程中,BM的中点N经过的路径长为m,AC的长为n,请直接写出![]() 的值.
的值.
【答案】(1)BE=3![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
(1)先说明AB=BF,然后再利用等腰直角三角形的性质求解即可;
(2)如图2:连接EF,过点G作GH⊥EF交EF的延长线于H.设BG=a,FG=b.先利用相似三角形的性质证得EF![]() GF,最后根据解直角三角形求得AB即可;
GF,最后根据解直角三角形求得AB即可;
(3)如图3:在AC上取一点T,使得AT=AB,连接BT,TM,取BT的中点J,连接NJ.
先证NJ//TM,NJ=TM,得到∠BJN=∠BTM=90°,进一步得到点N的运动轨边是线段![]() ,最后代入即可.
,最后代入即可.
解:(1)如图1中,
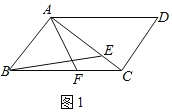
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAF=∠AFB
∵AF平分∠BAD,
∴∠DAF=∠BAF,
∴∠BAF=∠AFB,
∴AB=BF=3.
∵AB=AE,∠BAE=90°,
∴BE![]() AB=3
AB=3![]() .
.
(2)连接EF,过点G作GH⊥EF交EF的延长线于H.设BG=a,FG=b.
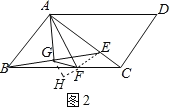
∵AB=AE,∠BAE=90°,BG=GE,
∴AG⊥BE,AG=GB=GE,
∴AB![]() BG
BG![]() a.
a.
∵BF=AB![]() a,
a,
∴BF2=2a2,BGBE=2a2,
∴BF2=BGBE,
∴![]() ,
,
∵∠FBG=∠EBF,
∴△GBF∽△FBE,
∴![]() ,∠BFG=∠BEF,
,∠BFG=∠BEF,
∴EF![]() GF
GF![]() b.
b.
∵∠BAF=∠BFA,∠GAF=∠BFG,
∴∠AFG=∠BAG=45°,∠GAF=∠GEF,
∴∠AGE=∠AFE=90°,
∴∠GFH=45°.
∵GH⊥EH,
∴GH=FH![]() b,
b,
∴EH=FH+EF![]() b,
b,
∴EG![]() b
b
∴AB=AE![]() GE
GE![]() b,
b,
∴AB![]() GF.
GF.
(3)如图3中,在AC上取一点T,使得AT=AB,连接BT,TM,取BT的中点J,连接NJ.
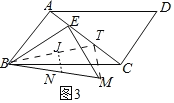
∵△ABT,△BEM都是等腰直角三角形,
∴BT![]() AB,BM
AB,BM![]() BE,∠ABT=∠EBM=45°,
BE,∠ABT=∠EBM=45°,
∴![]() ,∠ABE=∠TBM,
,∠ABE=∠TBM,
∴△ABE∽△TBM,
∴![]() ,∠AEB=∠BMT.
,∠AEB=∠BMT.
∵∠AEB+∠BET=180°,
∴∠BMT+∠BET=180°,
∴∠EBM+∠ETM=180°.
∵∠EBM=∠ETB=45°,
∴∠ETM=135°,∠BTM=90°.
∵BJ=JT,BN=NM,
∴NJ∥TM,NJ![]() TM,
TM,
∴∠BJN=∠BTM=90°,
∴点N的运动轨迹是线段JN,JN![]() TM
TM![]() AE.
AE.
∵点E从A运动到C时,AE=AC=n,
∴m![]() n,
n,
∴![]() .
.


科目:初中数学 来源: 题型:
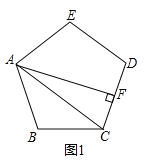
【题目】我们学过正多边形及其性质,了解了正多边形各边相等、各内角相等、具有轴对称性和旋转不变....下面我们继续探究正五边形相关线段及角的关系:
如图1,正五边形![]() 中,
中,
![]() 连接
连接![]() ,并作
,并作![]() ,则
,则![]() 度;
度;
![]() 连接
连接![]() 交
交![]() 于点
于点![]() ,求证:四边形
,求证:四边形![]() 是菱形;
是菱形;
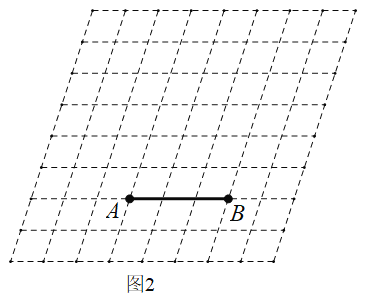
![]() 如图2,是一个斜网格图
如图2,是一个斜网格图![]() , 每个小菱形的较小内角是
, 每个小菱形的较小内角是![]() ,请利用一把角尺(只能画直角和直线,不能度量,可以用三角板替代)在网格图中画出以
,请利用一把角尺(只能画直角和直线,不能度量,可以用三角板替代)在网格图中画出以![]() 为一边的正五边形
为一边的正五边形![]() (保留作图痕迹).
(保留作图痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】朝阳公司以10元/千克的价格收购一批产品进行销售,经过市场调查发现:日销售量y(千克)与销售价格x(元/千克)之间是一次函数关系,当销售价格x是10元/千克时,日销售量y是300千克,当销售价格x是20元/千克时,日销售量y是150千克.
(1)求y与x之间的函数表达式;
(2)朝阳公司应该如何确定这批产品的销售价格,才能使日销售利润W1元最大?
(3)若朝阳公司每销售1千克这种产品需支出a元(a>0)的相关费用,当20≤x≤25时,公司的日获利W2元的最大值为1215元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,BC=12,E为AD中点,F为AB上一点,将△AEF沿EF折叠后,点A恰好落到CF上的点G处,则折痕EF的长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
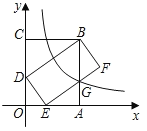
【题目】如图,矩形OABC的顶点A、C分别在x轴、y轴的正半轴上,点D在边OC上,且BD=OC,以BD为边向下作矩形BDEF,使得点E在边OA上,反比例函数y![]() (k≠0)的图象经过边EF与AB的交点G.若AG
(k≠0)的图象经过边EF与AB的交点G.若AG![]() ,DE=2,则k的值为____.
,DE=2,则k的值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
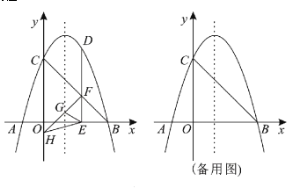
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)直接写出抛物线的解析式为:;
(2)点![]() 为第一象限内抛物线上的一动点,作
为第一象限内抛物线上的一动点,作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的垂线与抛物线的对称轴和
的垂线与抛物线的对称轴和![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
①求![]() 的最大值;
的最大值;
②连接![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人类的血型一般可分为A,B,AB,O型四种,宁波市中心血战2015年共有8万人无偿献血,血战统计人员由电脑随机选出20人,血型分别是:
O,A,O,B,O,A,A,AB,A,O,O,B,AB,B,O,A,O,B,O,A.
(1)请设计统计表分类统计这20人各类血型人数;
(2)若每位献血者平均献血200毫升,一年中宁波市各医院O型血用血量约为6×106毫米,请你估计2015年这8万人所献的O型血是否够用?
查看答案和解析>>
科目:初中数学 来源: 题型:
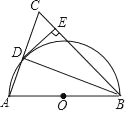
【题目】如图,在△ABC中,BA=BC,以AB为直径作⊙O,交AC于点D,连接DB,过点D作DE⊥BC,垂足为E.
(1)求证:AD=CD.
(2)求证:DE为⊙O的切线.
(3)若∠C=60°,DE=![]() ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com