
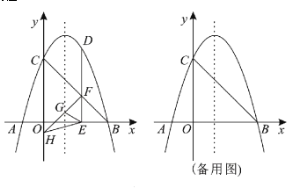
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)直接写出抛物线的解析式为:;
(2)点![]() 为第一象限内抛物线上的一动点,作
为第一象限内抛物线上的一动点,作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的垂线与抛物线的对称轴和
的垂线与抛物线的对称轴和![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
①求![]() 的最大值;
的最大值;
②连接![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() ,
,![]()
【解析】
(1)将点![]() ,
,![]() 代入抛物线
代入抛物线![]() ,求出b、c的值,继而求出抛物线解析式;
,求出b、c的值,继而求出抛物线解析式;
(2)①先求出点C的坐标,由待定系数法求出直线BC的解析式,作![]() 轴于点
轴于点![]() ,可得:
,可得: ![]() ,由线段的和差可得:
,由线段的和差可得:![]() ,代入数据得到二次函数,由二次函数的性质可知当
,代入数据得到二次函数,由二次函数的性质可知当![]() ,
,![]() 有最大值;
有最大值;
②作![]() 轴于点
轴于点![]() ,记直线
,记直线![]() 与
与![]() 轴交于点
轴交于点![]() ,易知
,易知![]() ,由等角对等边可知:EN=EF,OH=ON,由抛物线的性质可得MG=1,继而可得HG=
,由等角对等边可知:EN=EF,OH=ON,由抛物线的性质可得MG=1,继而可得HG=![]() ,根据相似三角形的判定及其性质可得
,根据相似三角形的判定及其性质可得![]() ,
,![]() ,代入数据可得
,代入数据可得![]() ,在
,在![]() 中,由勾股定理可得
中,由勾股定理可得![]() ,可得一元二次方程,继而解方程求解.
,可得一元二次方程,继而解方程求解.
(1)将点![]() ,
,![]() 代入抛物线
代入抛物线![]() 得:
得:
![]()
解得:![]()
故抛物线的解析式为:![]() ;
;
(2)①当![]() 时,
时,![]()
![]() 点
点![]() ,又
,又![]() 点
点![]() ,
,
![]() 的解析式为:
的解析式为:![]() ,
,
![]() ,
,
![]() ,
,
作![]() 轴于点
轴于点![]() ,又
,又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
化简得:![]() ,
,
由题意有![]() ,且
,且![]() ,
,![]() ,
,
![]() 当
当![]() 时,
时,![]() 取最大值,
取最大值,
![]() 的最大值为
的最大值为![]()
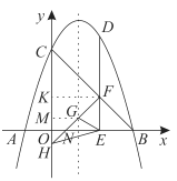
②作![]() 轴于点
轴于点![]() ,记直线
,记直线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
![]() 轴,
轴,![]() 轴,
轴,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() 的对称轴为
的对称轴为![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,又∠EHF=∠GHE,
,又∠EHF=∠GHE,
![]() ,
,
![]() ,
,
![]()
在![]() 中,
中,![]() ,
,![]()
![]()
![]() ,
,
解得:![]() 或
或![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的一点.
边上的一点.
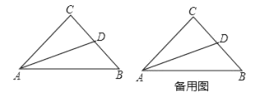
(1)以点![]() 为旋转中心,将
为旋转中心,将![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() ,请你画出旋转后的图形;
,请你画出旋转后的图形;
(2)延长![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)若![]() ,
,![]() ,连接
,连接![]() ,请直接写出
,请直接写出![]() 的长度______________.
的长度______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备为“中国古诗词”朗诵比赛购买奖品.已知在中央商场购买3个甲种奖品和2个乙种奖品共需120元;购买5个甲种奖品和4个乙种奖品共需210元.
(1)求甲、乙两种奖品的单价;
(2)学校计划购买甲、乙两种奖品共80个,且此次购买奖品的费用不超过1500元.正逢中央商场促销,所有商品一律八折销售,求学校在中央商场最多能购买多少个甲种奖品?
查看答案和解析>>
科目:初中数学 来源: 题型:
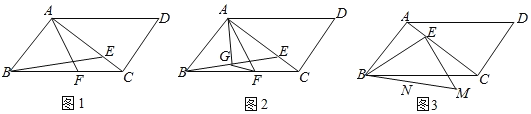
【题目】在ABCD中,AF平分∠BAD交BC于点F,∠BAC=90°,点E是对角线AC上的点,连结BE.
(1)如图1,若AB=AE,BF=3,求BE的长;
(2)如图2,若AB=AE,点G是BE的中点,∠FAG=∠BFG,求证:AB![]() FG;
FG;
(3)如图3,以点E为直角顶点,在BE的右下方作等腰直角△BEM,若点E从点A出发,沿AC运动到点C停止,设在点E运动过程中,BM的中点N经过的路径长为m,AC的长为n,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
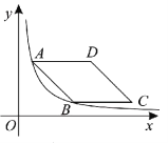
【题目】如图,在平面直角坐标系中,菱形![]() 在第一象限内,边
在第一象限内,边![]() 与
与![]() 轴平行,
轴平行,![]() ,
,![]() 两点的纵坐标分别为
两点的纵坐标分别为![]() ,
,![]() ,反比例函数
,反比例函数![]() 的图象经过
的图象经过![]() ,
,![]() 两点,菱形
两点,菱形![]() 的面积为
的面积为![]() ,则
,则![]() 的值为________.
的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
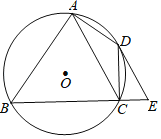
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=8,CE=2时,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为报答当年5.12汶川地震各地的驰援深情,四川某农产品公司决定将本公司农业基地生产的蔬菜水果全部运到湖北武汉,支援武汉人民抗击新冠疫情.为了运输的方便,将蔬菜和水果分别打包成件,蔬菜和水果共260件,蔬菜比水果多40件.
(1)求打包成件的蔬菜和水果各多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批物资全部运往武汉.已知甲种货车最多可装蔬菜30件和水果13件,乙种货车最多可装蔬菜和水果各15件.如果甲种货车每辆需付运输费3000元,乙种货车每辆需付运输费2400元.则公司安排甲、乙两种货车时有几种方案?并说明公司选择哪种方案可使运输费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把分子为1的分数叫做单位分数,如:![]() ,
,![]() ,
,![]() ,任何一个单位分数都可以拆分成两个不同的单位分数的和,如“
,任何一个单位分数都可以拆分成两个不同的单位分数的和,如“![]() =
=![]() +
+![]() ”,“
”,“![]() =
=![]() +
+![]() ”……
”……
(1)根据对上述式子的观察,你会发现.![]() =
=![]() ·请将问题中的空格补充完整.
·请将问题中的空格补充完整.
(2)进一步思考,单位分数![]() (n是不小于2的正整数),请写出■和●所表示的代数式,并对你的结论进行验证.
(n是不小于2的正整数),请写出■和●所表示的代数式,并对你的结论进行验证.
(3)请用(2)中你找出的规律解方程![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com