
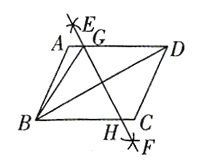
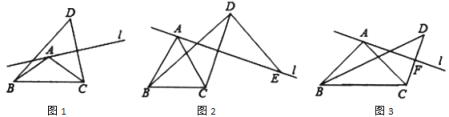
【题目】如图.已知四边形ABCD是平行四边形,结合作图痕迹,下列说法不正确的是( )
A.![]() 与
与![]() 垂直
垂直
B.![]()
C.![]() 平分
平分![]()
D.若![]() 的周长为4,则平行四边形
的周长为4,则平行四边形![]() 的周长为8
的周长为8
【答案】C
【解析】
设EF与BD的交点为点O,由作图痕迹可得,直线EF是BD的垂直平分线,故A正确;证明△DOG≌△BOH,得到GD=HB,进而可得B正确;求出![]() 平分∠GBC可得C错误;根据AB+AG+BG=AB+AG+GD=AB+AD=4,可得平行四边形
平分∠GBC可得C错误;根据AB+AG+BG=AB+AG+GD=AB+AD=4,可得平行四边形![]() 的周长为8,即D正确.
的周长为8,即D正确.
解:设EF与BD的交点为点O,由作图痕迹可得,直线EF是BD的垂直平分线,
∴![]() 与
与![]() 垂直,A选项说法正确;
垂直,A选项说法正确;
∵AD∥BC,EF是BD的垂直平分线,
∴∠GDB=∠DBH,DO=BO,
又∵∠GOD=∠BOH,
∴△DOG≌△BOH,
∴GD=HB,
∴![]() ,B选项说法正确;
,B选项说法正确;
∵EF垂直平分BD,
∴BG=DG,
∴∠GBD=∠GDB,
又∵∠GDB=∠DBH,
∴∠GBD=∠DBH,
∴![]() 平分∠GBC,
平分∠GBC,
∵∠ABC=∠ADC≠∠GBC,
∴C选项说法错误;
∵![]() 的周长为4,BG=GD,
的周长为4,BG=GD,
∴AB+AG+BG=AB+AG+GD=AB+AD=4,
∴平行四边形![]() 的周长=2×(AB+ AD)=8,D选项说法正确,
的周长=2×(AB+ AD)=8,D选项说法正确,
故选:C.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
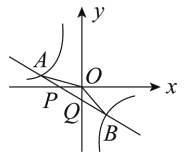
【题目】如图,已知直线![]() 与
与![]() 轴、
轴、![]() 轴相交于
轴相交于![]() 、
、![]() 两点,与
两点,与![]() 的图象相交于
的图象相交于![]() 、
、![]() 两点,连接
两点,连接![]() 、
、![]() .给出下列结论:
.给出下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④不等式
;④不等式![]() 的解集是
的解集是![]() 或
或![]() .
.
其中正确结论的序号是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
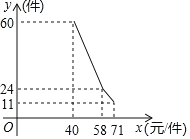
【题目】某店因为经营不善欠下38000元的无息贷款的债务,想转行经营服装专卖店又缺少资金.“中国梦想秀”栏目组决定借给该店30000元资金,并约定利用经营的利润偿还债务(所有债务均不计利息)已知该店代理的某品牌服装的进价为每件40元,该品牌服装日的售量y(件)与销售价x(元/件)之间的关系可用图中的一条折线(实线)来表示.
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)当销售价为多少元时,该店的日销售利润最大;
(3)该店每天支付工资和其它费用共250元,该店能否在一年内还清所有债务.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB为![]() 的直径,
的直径,![]() 为圆弧上的一点,
为圆弧上的一点,![]() ,垂足为D,AC平分
,垂足为D,AC平分![]() ,AB的延长线交直线
,AB的延长线交直线![]() 于点
于点![]() .
.
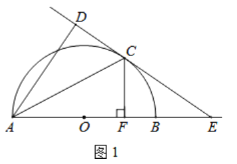
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,B为
,B为![]() 的中点,
的中点,![]() ,垂足为点
,垂足为点![]() ,求
,求![]() 的长;
的长;
(3)如图2,连接OD交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
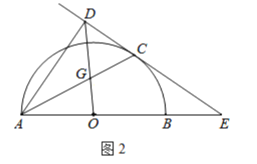
【题目】已知在![]() 中,
中,![]() ,直线
,直线![]() 经过点
经过点![]() (不经过点
(不经过点![]() 或点
或点![]() ),点
),点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() .
.
(1)如图1,根据已知可以判断点![]() 在以点
在以点![]() 为圆心,
为圆心,![]() 为半径的圆上.请你直接写出
为半径的圆上.请你直接写出![]() 的度数(用含
的度数(用含![]() 的式子表示).
的式子表示).
(2)如图2,当![]() 时,过点
时,过点![]() 作
作![]() 的垂线与直线
的垂线与直线![]() 交于点
交于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,当![]() 时,记直线
时,记直线![]() 与
与![]() 的交点为
的交点为![]() ,连接
,连接![]() .将直线
.将直线![]() 绕点
绕点![]() 旋转,当线段
旋转,当线段![]() 的长取得最大值时,直接写出
的长取得最大值时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业对一种设备进行升级改造,并在一定时间内进行生产营销,设改造设备的台数为x,现有甲、乙两种改造方案.
甲方案:升级后每台设备的生产营销利润为4000元,但改造支出费用![]() 由材料费和施工费以及其他费用三部分组成,其中材料费与x的平方成正比,施工费与x成正比,其他费用为2500元,(利润=生产营销利润-改造支出费用).设甲方案的利润为
由材料费和施工费以及其他费用三部分组成,其中材料费与x的平方成正比,施工费与x成正比,其他费用为2500元,(利润=生产营销利润-改造支出费用).设甲方案的利润为![]() (元),经过统计,得到如下数据:
(元),经过统计,得到如下数据:
改造设备台数x(台) | 20 | 40 |
利润 | 9500 | 5500 |
乙方案:升级后每台设备的生产营销利润为3500元,但改造支出费用![]() 与x之间满足函数关系式:
与x之间满足函数关系式:![]() (a为常数,
(a为常数,![]() ),且在使用过程中一共还需支出维护费用
),且在使用过程中一共还需支出维护费用![]() ,(利润=生产营销利润-改造支出费用-维护费用).设乙方案的利润为
,(利润=生产营销利润-改造支出费用-维护费用).设乙方案的利润为![]() (元).
(元).
(1)分别求出![]() ,
,![]() 与x的函数关系式;
与x的函数关系式;
(2)若![]() ,
,![]() 的最大值相等,求a的值;
的最大值相等,求a的值;
(3)如果要将30台设备升级改造,请你帮助决策,该企业应选哪种方案,所获得的利润较大.
查看答案和解析>>
科目:初中数学 来源: 题型:
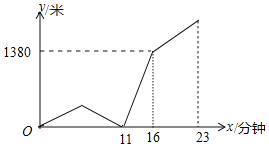
【题目】一天,小明从家出发匀速步行去学校上学.几分钟后,在家休假的爸爸发现小明忘带数学书,于是爸爸立即匀速跑步去追小明,爸爸追上小明后以原速原路跑回家.小明拿到书后以原速的![]() 快步赶往学校,并在从家出发后23分钟到校(小明被爸爸追上时交流时间忽略不计).两人之间相距的路程y(米)与小明从家出发到学校的步行时间x(分钟)之间的函数关系如图所示,则小明家到学校的路程为________米.
快步赶往学校,并在从家出发后23分钟到校(小明被爸爸追上时交流时间忽略不计).两人之间相距的路程y(米)与小明从家出发到学校的步行时间x(分钟)之间的函数关系如图所示,则小明家到学校的路程为________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究)
(1)观察下列算式,并完成填空:
1=12
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+…+(2n-1)=______.(n是正整数)
(2)如图是某市一广场用正六边形、正方形和正三角形地板砖铺设的图案,图案中央是一块正六边形地板砖,周围是正方形和正三角形的地板砖.从里向外第一层包括6块正方形和6块正三角形地板砖;第二层包括6块正方形和18块正三角形地板砖;以此递推.
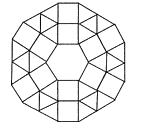
①第3层中分别含有______块正方形和______块正三角形地板砖;
②第n层中含有______块正三角形地板砖(用含n的代数式表示).
(应用)
该市打算在一个新建广场中央,采用如图样式的图案铺设地面,现有1块正六边形、150块正方形和420块正三角形地板砖,问:铺设这样的图案,最多能铺多少层?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为今年将要参加中考的好友小李制作了一个(如图)正方体礼品盒,六面上各有一字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的平面展开图可能是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com