
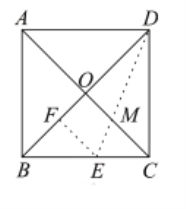
【题目】如图,边长为![]() 的正方形
的正方形![]() 的对角线
的对角线![]() 与
与![]() 交于点
交于点![]() ,将正方形
,将正方形![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕
处,折痕![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
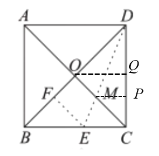
过点M作MP⊥CD垂足为P,过点O作OQ⊥CD垂足为Q,根据正方形的性质得到AB=AD=BC=CD=2,∠DCB=∠COD=∠BOC=90°,根据折叠的性质得到∠EDF=∠CDF,设OM=PM=x,根据相似三角形的性质即可求解.
过点M作MP⊥CD垂足为P,过点O作OQ⊥CD垂足为Q,
∵ 正方形的边长为2,
∴OD=OC=![]() , OQ=DQ=1 ,
, OQ=DQ=1 ,
由折叠可知,∠EDF=∠CDF,
又∵AC⊥BD, ∴OM=PM,
设OM=PM=x,则CM=![]() -x,
-x,
∵OQ⊥CD,MP⊥CD,
∴∠OQC=∠MPC=90°, ∠PCM=∠QCO,
∴△CMP∽△COQ,
∴![]() , 即
, 即![]() ,
,
解得: ![]() ,
,
∴OM=PM=![]() .
.
故选:D.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】[问题提出]
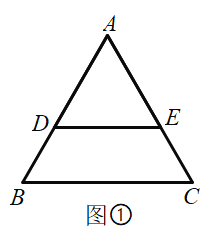
(1)如图![]() 均为等边三角形,点
均为等边三角形,点![]() 分别在边
分别在边![]() 上.将
上.将![]() 绕点
绕点![]() 沿顺时针方向旋转,连结
沿顺时针方向旋转,连结![]() .在图
.在图![]() 中证明
中证明![]() .
.

[学以致用]
(2)在![]() 的条件下,当点
的条件下,当点![]() 在同一条直线上时,
在同一条直线上时,![]() 的大小为 度.
的大小为 度.
[拓展延伸]
(3)在![]() 的条件下,连结
的条件下,连结![]() .若
.若![]() 直接写出
直接写出![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程![]()
(1)求证:不论k取什么实数值,这个方程总有实数根;
(2)若等腰三角形ABC的一边长为![]() ,另两边的长b、c恰好是这个方程的两个根,求△ABC的周长.
,另两边的长b、c恰好是这个方程的两个根,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,滑动调节式遮阳伞的立柱AC垂直于地面AB,P为立柱上的滑动调节点,伞体的截面示意图为△PDE,F为PD的中点,AC=2.8m,PD=2m,CF=1m,∠DPE=15°.根据生活经验,当太阳光线与PE垂直时,遮阳效果最佳,在上午10:00时,太阳光线与地面的夹角为65°,若要遮阳效果最佳AP的长约为( )
(参考数据:sin65°≈0.91,cos65°≈0.42,sin50°≈0.77,cos50°≈0.64)

A.1.2mB.1.3mC.1.5mD.2.0m
查看答案和解析>>
科目:初中数学 来源: 题型:
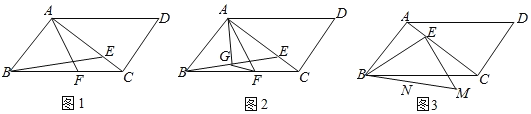
【题目】在ABCD中,AF平分∠BAD交BC于点F,∠BAC=90°,点E是对角线AC上的点,连结BE.
(1)如图1,若AB=AE,BF=3,求BE的长;
(2)如图2,若AB=AE,点G是BE的中点,∠FAG=∠BFG,求证:AB![]() FG;
FG;
(3)如图3,以点E为直角顶点,在BE的右下方作等腰直角△BEM,若点E从点A出发,沿AC运动到点C停止,设在点E运动过程中,BM的中点N经过的路径长为m,AC的长为n,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在开展“健康中国”读书征文评比活动中,对优秀征文予以评奖,并颁发奖品,奖品有甲、乙、丙三种类型.已知![]() 个丙种奖品的价格是
个丙种奖品的价格是![]() 个甲种奖品价格的
个甲种奖品价格的![]() 倍,
倍,![]() 个乙种奖品的价格比
个乙种奖品的价格比![]() 个甲种奖品的价格多
个甲种奖品的价格多![]() 元.用
元.用![]() 元分别去购买甲、乙、丙三种奖品,购买到甲和丙两种奖品的总数量是乙种奖品数量的
元分别去购买甲、乙、丙三种奖品,购买到甲和丙两种奖品的总数量是乙种奖品数量的![]() 倍.
倍.
(1)求![]() 个甲、乙、丙三种奖品的价格分别是多少元?
个甲、乙、丙三种奖品的价格分别是多少元?
(2)该校计划:购买甲、乙、丙三种奖品共![]() 个,其中购买甲种奖品的数量是丙种奖品的
个,其中购买甲种奖品的数量是丙种奖品的![]() 倍,且甲种奖品的数量不少于乙、丙两种奖品的数量之和.求该校完成购买计划最多要花费多少元?
倍,且甲种奖品的数量不少于乙、丙两种奖品的数量之和.求该校完成购买计划最多要花费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
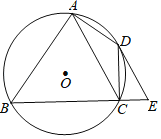
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=8,CE=2时,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m3)随之变化,已知气体的密度ρ与体积V是反比例函数关系,它的图象如图所示.
(1) 求密度ρ关于体积V的函数解析式;
(2) 当V=9m3时,求二氧化碳的密度ρ.

查看答案和解析>>
科目:初中数学 来源: 题型:
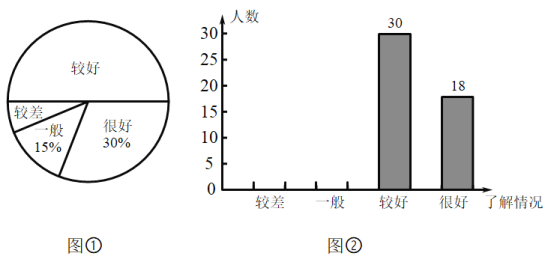
【题目】“安全教育,警钟长鸣”,为此,某校随机抽取了九年级(1)班的学生对安全知识的了解情况进行了一次调查统计.图①和图②是通过数据收集后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(1)九年级(1)班共有多少名学生;
(2)补全图②;
(3)在扇形统计图中,对安全知识的了解情况为“较差”部分所对应的圆心角的度数是多少;
(4)若全校有1500名学生,估计对安全知识的了解情况为“较差”、“一般”的学生共有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com