
【题目】如图,在平面直角坐标系xoy中,直线![]() 与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是
与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是![]() ,且经过A、C两点,与x轴的另一交点为点B.
,且经过A、C两点,与x轴的另一交点为点B.
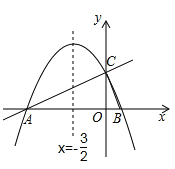
(1)①直接写出点B的坐标;
②求抛物线解析式.
(2)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
【答案】(1) B的坐标为(1,0).y=-![]() x2-
x2-![]() x+2.(2)4, P(-2,3).
x+2.(2)4, P(-2,3).
【解析】
试题分析:(1)①先求的直线y=![]() x+2与x轴交点的坐标,然后利用抛物线的对称性可求得点B的坐标;②设抛物线的解析式为y=y=a(x+4)(x-1),然后将点C的坐标代入即可求得a的值;
x+2与x轴交点的坐标,然后利用抛物线的对称性可求得点B的坐标;②设抛物线的解析式为y=y=a(x+4)(x-1),然后将点C的坐标代入即可求得a的值;
(2)设点P、Q的横坐标为m,分别求得点P、Q的纵坐标,从而可得到线段PQ=-![]() m2-2m,然后利用三角形的面积公式可求得S△PAC=
m2-2m,然后利用三角形的面积公式可求得S△PAC=![]() ×PQ×4,然后利用配方法可求得△PAC的面积的最大值以及此时m的值,从而可求得点P的坐标;
×PQ×4,然后利用配方法可求得△PAC的面积的最大值以及此时m的值,从而可求得点P的坐标;
试题解析:(1)①y=![]() x+2当x=0时,y=2,当y=0时,x=-4,
x+2当x=0时,y=2,当y=0时,x=-4,
∴C(0,2),A(-4,0),
由抛物线的对称性可知:点A与点B关于x=-![]() 对称,
对称,
∴点B的坐标为(1,0).
②∵抛物线y=ax2+bx+c过A(-4,0),B(1,0),
∴可设抛物线解析式为y=a(x+4)(x-1),
又∵抛物线过点C(0,2),
∴2=-4a
∴a=-![]()
∴y=-![]() x2-
x2-![]() x+2.
x+2.
(2)设P(m,-![]() m2-
m2-![]() m+2).
m+2).
过点P作PQ⊥x轴交AC于点Q,
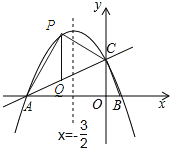
∴Q(m,![]() m+2),
m+2),
∴PQ=-![]() m2-
m2-![]() m+2-(
m+2-(![]() m+2)
m+2)
=-![]() m2-2m,
m2-2m,
∵S△PAC=![]() ×PQ×4,
×PQ×4,
=2PQ=-m2-4m=-(m+2)2+4,
∴当m=-2时,△PAC的面积有最大值是4,
此时P(-2,3).


科目:初中数学 来源: 题型:
【题目】在平静的湖面上,有一支红莲,高出水面1米,阵风吹来,红莲被吹到一边,花朵齐及水面,已知红莲移动的水平距离为2米,问这里水深是( )
A. 1米 B. 1.5米 C. 2米 D. 2.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市一月份的营业额为36万元,三月份的营业额为48万元,设每月的平均增长率为x,则可列方程为( )
A. 48(1﹣x)2=36 B. 48(1+x)2=36 C. 36(1﹣x)2=48 D. 36(1+x)2=48
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+px+q=0的两根同为负数,则( )
A. p>0且q>0 B. p>0且q<0 C. p<0且q>0 D. p<0且q<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程x2-8x-1=0配方后可变形为( )
A. (x+4)2=17 B. (x+4)2=15 C. (x-4)2=17 D. (x-4)2=15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场新进一批商品,每个成本价25元,销售一段时间发现销售量y(个)与销售单价x(元/个)之间成一次函数关系,如下表:
x(元/个) | 30 | 50 |
y(个) | 190 | 150 |
(1)求y与x之间的函数关系式;
(2)若该商品的销售单价在45元~80元之间浮动,
①销售单价定为多少元时,销售利润最大?此时销售量为多少?
②商场想要在这段时间内获得4 550元的销售利润,销售单价应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com