
为了响应政府提出的由中国制造向中国创造转型的号召,某公司自主设计了一款成本为40元的可控温杯,并投放市场进行试销售,经过调查发现该产品每天的销售量y(件)与销售单价x(元)满足一次函数关系:y=﹣10x+1200.
(1)求出利润S(元)与销售单价x(元)之间的关系式(利润=销售额﹣成本);
(2)当销售单价定为多少时,该公司每天获取的利润最大?最大利润是多少元?
科目:初中数学 来源: 题型:
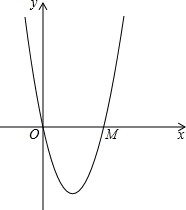
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a>0)与x轴交于点O、M.对称轴为直线x=2,以OM为直径作圆A,以OM的长为边长作菱形ABCD,且点B、C在第四象限,点C在抛物线对称轴上,点D在y轴负半轴上;
(1)求证:4a+b=0;
(2)若圆A与线段AB的交点为E,试判断直线DE与圆A的位置关系,并说明你的理由;
(3)若抛物线顶点P在菱形ABCD的内部且∠OPM为锐角时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
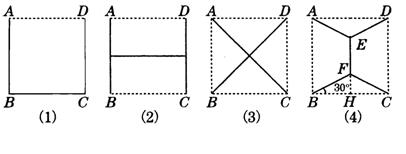
国家电力总公司为了改善农村用电电费过高的现状,目前正在全国各地农村进行电网改造,某地有四个村庄A、B、C、D,且正好位于一个正方形的四个顶点,现计划在四个村庄联合架设一条线路,他们设计了四种架设方案,如图实线部分.请你帮助计算一下,哪种架设方案最省电线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com