
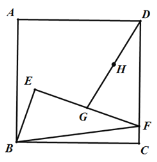
【题目】如图,E为正方形ABCD内一点,点F在CD边上,且∠BEF=90°,EF=2BE.点G为EF的中点,点H为DG的中点,连接EH并延长到点P,使得PH=EH,连接DP.
(1)依题意补全图形;
(2)求证:DP=BE;
(3)连接EC,CP,猜想线段EC和CP的数量关系并证明.
【答案】(1)详见解析;(2)详见解析;(3)详见解析
【解析】
(1)根据题意可以画出完整的图形;
(2)由EF=2BE,点G为EF的中点可知,要证明DP=BE,只要证明DP=EG即可,要证明DP=EG,只要证明ΔPDH≌ΔEGH即可,然后根据题目中的条件和全等三角形的判定即可证明结论成立;
(3)首先写出线段EC和CP的数量关系,然后利用全等三角形的判定和性质即可证明结论成立.
解:(1)依题意补全图形如下:
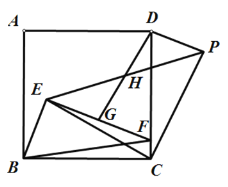
(2)∵点H为线段DG的中点,
∴DH=GH.
在ΔPDH和ΔEGH中,
∵EH=PH,∠EHG=∠PHD,
∴ΔPDH≌ΔEGH(SAS).
∴DP=EG.
∵G为EF的中点,
∴EF=2EG.
∵EF=2EB,
∴BE=EG=DP.
(3)猜想:EC=CP.
由(2)可知ΔPDH≌ΔEGH.
∴∠HEG=∠HPD.
∴DP∥EF.
∴∠PDC=∠DFE.
又∵∠BEF=∠BCD=90°,
∴∠EBC+∠EFC=180°.
又∵∠DFE+∠EFC=180°,
∴∠EBC=∠DFE=∠PDC.
∵BC=DC,DP=BE,
∴ΔEBC≌ΔPDC(SAS).
∴EC=PC.
故答案为:(1)详见解析;(2)详见解析;(3)详见解析.


科目:初中数学 来源: 题型:
【题目】已知,如图A、B分别为数轴上的两点,A点对应的数为-20,B点对应的数为80.

(1)请写出AB的中点M对应的数.
(2)现在有一只电子蚂蚁P从B点出发,以2个单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以3个单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的C点相遇,
①你知道经过几秒两只电子蚂蚁相遇?
②点C对应的数是多少?
③经过多长时间两只电子蚂蚁在数轴上相距15个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 要比较a与b的大小,可以先求a与b的差,再看这个差是正数、负数还是零.由此可见,要判断两个式子值的大小,只要考虑它们的差就可以了.
已知A=16a2+a+15 , B=4a2+![]() a+7 , C=a2+
a+7 , C=a2+![]() a+4.
a+4.
请你按照上述文字提供的信息:(1)试比较A与2B的大小; (2)试比较2B与3C的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标为(m,n),若点A′(m,n′)的纵坐标满足n′=![]() ,则称点A′是点A的“绝对点”.
,则称点A′是点A的“绝对点”.
(1)点(3,2)的“绝对点”的坐标为 .
(2)点P是函数y=4x-1的图象上的一点,点P′是点P的“绝对点”.若点P与点P′重合,求点P的坐标.
(3)点Q(a,b)的“绝对点”Q′是函数y=2x2的图象上的一点.当0≤a≤2 时,求线段QQ′的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底部未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分周长和是_________(用代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点的位置如图所示,点A′的坐标是(﹣2,2),现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
(1)请画出平移后的△A′B′C′(不写画法);
(2)并直接写出点B′、C′的坐标:B′( )、C′( );
(3)若△ABC内部一点P的坐标为(a,b),则点P的对应点P′的坐标是( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
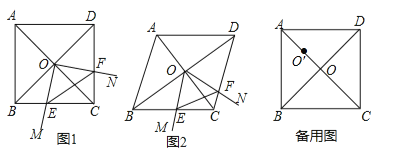
【题目】(12分)菱形ABCD中,两条对角线AC,BD相交于点O,∠MON+∠BCD=180°,∠MON绕点O旋转,射线OM交边BC于点E,射线ON交边DC于点F,连接EF.
(1)如图1,当∠ABC=90°时,△OEF的形状是 ;
(2)如图2,当∠ABC=60°时,请判断△OEF的形状,并说明理由;
(3)在(1)的条件下,将∠MON的顶点移到AO的中点O′处,∠MO′N绕点O′旋转,仍满足∠MO′N+∠BCD=180°,射线O′M交直线BC于点E,射线O′N交直线CD于点F,当BC=4,且![]() 时,直接写出线段CE的长.
时,直接写出线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com