
【题目】已知:P是正方形ABCD对角线BD上一点,PE⊥DC,PF⊥BC,E、F分别为垂足.
求证:AP=EF.
【答案】证明:如图,连接PC,
∵PE⊥DC,PF⊥BC,四边形ABCD是正方形,
∴∠PEC=∠PFC=∠ECF=90°,
∴四边形PECF为矩形,
∴PC=EF,
又∵P为BD上任意一点,
∴PA、PC关于BD对称,
可以得出,PA=PC,所以EF=AP.
【解析】利用正方形的关于对角线成轴对称,利用轴对称的性质可得出EF=AP.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图所示)
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?
(6)他由离家最远的地方返回时的平均速度是多少?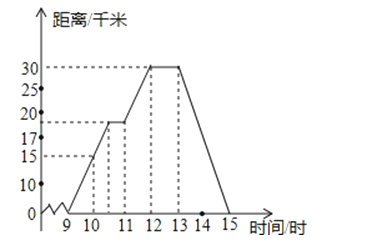
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在正方形ABCD中,对角线AC与BD相交于点O,OE∥AB交BC于点E,若AD=8cm,则OE的长为( )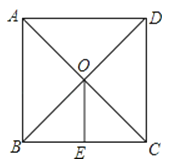
A.3cm
B.4cm
C.6cm
D.8cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形ABCD中,AB=1,点P是对角线AC上的一点,分别以AP,PC为对角线作正方形,则两个小正方形的周长的和是( )
A.2
B.4
C.6
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个矩形的面积为(6ab2-4a2b),一边长为2ab,则它的另一边长为( )
A. 3b-2a B. 3b2+2a C. 3b2-4a2 D. 3b-2a2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、C、E是同一直线上的三点,四边形ABCD与四边形CEFG都是正方形,连接BG、DE.
(1)求证:BG=DE;
(2)已知小正方形CEFG的边长为1cm,连接CF,如果将正方形CEFG绕点C逆时针旋转,当A、E两点之间的距离最小时,求线段CF所扫过的面积.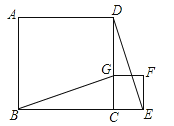
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形纸片.把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF.若CD=6,则AF等于( )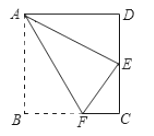
A.![]()
B.![]()
C.![]()
D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com