
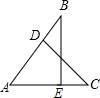
 如图,AB=AC,∠AEB=∠ADC=90°,则判断△ABE≌△ACD的方法是( )
如图,AB=AC,∠AEB=∠ADC=90°,则判断△ABE≌△ACD的方法是( )| A. | AAS | B. | HL | C. | SSS | D. | SAS |
分析 根据三角形内角和定理得出∠A+∠B=90°,∠C+∠A=90°,求出∠B=∠C,根据全等三角形的判定定理推出即可.
解答 解:∵∠AEB=∠ADC=90°,
∴∠A+∠B=90°,∠C+∠A=90°,
∴∠B=∠C,
在△ABE和△ACD中,
$\left\{\begin{array}{l}{∠AEB=∠ADC}\\{∠B=∠C}\\{AB=AC}\end{array}\right.$,
∴△ABE≌△ACD(AAS).
故选A.
点评 本题考查了全等三角形的判定定理的应用,能正确运用判定定理进行推理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,直角三角形全等还有HL.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,二次函数y=ax2+bx+c图象的对称轴是x=$\frac{1}{3}$,下面四条信息:①abc<0,②a+2b+4c<0,③2a+3b=0,④2c>5b.你认为其中正确的有( )
如图,二次函数y=ax2+bx+c图象的对称轴是x=$\frac{1}{3}$,下面四条信息:①abc<0,②a+2b+4c<0,③2a+3b=0,④2c>5b.你认为其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
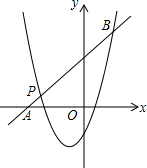 已知二次函数y=x2+mx+n的图象经过点P(-3,1),对称轴是经过(-1,0)且平行于y轴的直线.
已知二次函数y=x2+mx+n的图象经过点P(-3,1),对称轴是经过(-1,0)且平行于y轴的直线.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | (60,0) | B. | (72,0) | C. | (67$\frac{1}{5}$,$\frac{9}{5}$) | D. | (79$\frac{1}{5}$,$\frac{9}{5}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 南京市与连云港市两地相距300km,甲车在南京市,乙车在连云港市,两车同时出发,相向而行,在A地相遇.为节约费用(两车相遇并换货后,均需按原路返回出发地).两车换货后,甲车立即按原路返回南京市,而乙车又停留1小时后按原路返回连云港市.设每车在行驶过程中速度保持不变,两车间的距离y(km)与时间x(h)的函数关系如图所示,根据所提供的信息,回答下列问题:
南京市与连云港市两地相距300km,甲车在南京市,乙车在连云港市,两车同时出发,相向而行,在A地相遇.为节约费用(两车相遇并换货后,均需按原路返回出发地).两车换货后,甲车立即按原路返回南京市,而乙车又停留1小时后按原路返回连云港市.设每车在行驶过程中速度保持不变,两车间的距离y(km)与时间x(h)的函数关系如图所示,根据所提供的信息,回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com