
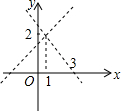 如图,不解关于x,y的方程组$\left\{\begin{array}{l}{y=x+1}\\{y=mx+n}\end{array}\right.$,请直接写出它的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
如图,不解关于x,y的方程组$\left\{\begin{array}{l}{y=x+1}\\{y=mx+n}\end{array}\right.$,请直接写出它的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$. 分析 根据两个函数的交点(1,2)可得方程组的解.
解答 解:∵y=x+1和y=mx+n的交点是(1,2),
∴方程组$\left\{\begin{array}{l}{y=x+1}\\{y=mx+n}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
故答案为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
点评 此题主要考查了一次函数与二元一次方程组的关系,关键是掌握两个一次函数的交点坐标是有两个函数解析式所组成的方程组的解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
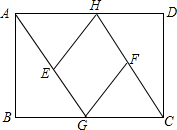 如图,在矩形ABCD中,H是AD上任意一点,AG∥CH交BC于点G,点E、F分别为AG、CH的中点,连接HE、FG.
如图,在矩形ABCD中,H是AD上任意一点,AG∥CH交BC于点G,点E、F分别为AG、CH的中点,连接HE、FG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
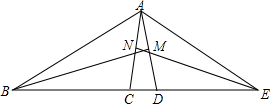 如图,已知点B,C,D,E在同一条直线上,BM,EN分别垂直平分AD,AC于M,N.
如图,已知点B,C,D,E在同一条直线上,BM,EN分别垂直平分AD,AC于M,N.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
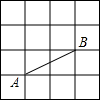 如图是正方形网格,除A,B两点外,在网格的格点上任取一点C,连接AC,BC,能使△ABC为等腰三角形的概率是( )
如图是正方形网格,除A,B两点外,在网格的格点上任取一点C,连接AC,BC,能使△ABC为等腰三角形的概率是( )| A. | $\frac{4}{23}$ | B. | $\frac{6}{23}$ | C. | $\frac{7}{23}$ | D. | $\frac{8}{23}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
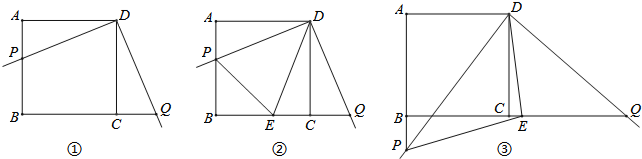
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
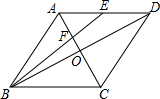 如图,菱形ABCD中,对角线AC与BD交于点O,点E为AD中点,连接BE交AC于点F,则$\frac{AF}{OF}$的值为( )
如图,菱形ABCD中,对角线AC与BD交于点O,点E为AD中点,连接BE交AC于点F,则$\frac{AF}{OF}$的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
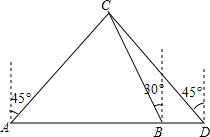 某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西30°,又航行了半小时到D处,望见灯塔C恰在西北方向,若船速为每小时20海里.求A、D两点间的距离.(结果不取近似值)
某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西30°,又航行了半小时到D处,望见灯塔C恰在西北方向,若船速为每小时20海里.求A、D两点间的距离.(结果不取近似值)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com