
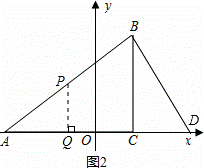
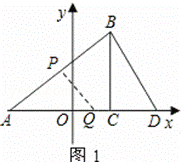
已知:如图,在平面直角坐标系中,△ABC是直角三角形,
∠ACB=90°,点A,C的坐标分别为A(﹣3,0),C(1,0),tan∠BAC= .
.
(1)写出点B的坐标;
(2)在x轴上找一点D,连接BD,使得△ADB与△ABC相似(不包括全等),并
求点D的坐标;
(3)在(2)的条件下,如P,Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,
问是否存在这样的m使得△APQ与△ADB相似?如存在,请求出的m值;
如不存在,请说明理由.

解:(1)B(1,3), (1分)
(2)如图1,过点B作BD⊥AB,交x轴于点D,
在Rt△ABC和Rt△ADB中,
∵∠BAC=∠DAB,
∴Rt△ABC∽Rt△ADB,
∴D点为所求,
又tan∠ADB=tan∠ABC=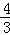 ,
,
∴CD=BC÷tan∠ADB=3÷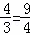 ,
,
∴OD=OC+CD=1+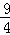 =
=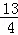 ,
,
∴D( 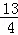 ,0); (4分)
,0); (4分)
(3)这样的m存在.
在Rt△ABC中,由勾股定理得AB=5,
如图1,当PQ∥BD时,△APQ∽△ABD,
则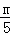 =
= ,
,
解得m=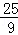 , (6分)
, (6分)
如图2,当PQ⊥AD时,△APQ∽△ADB,
则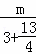 =
=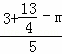 ,
,
解得m=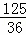 . (9分)
. (9分)
故存在m的值是 或
或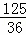 时,使得△APQ与△ADB相似.(10分)
时,使得△APQ与△ADB相似.(10分)


科目:初中数学 来源: 题型:
根据下面给出的数轴,解答下面的问题:(本题6分)
 |
⑴ 请你根据图中A、B两点的位置,分别写出它们所表示的有理数A: B: ;
⑵ 观察数轴,与点A的距离为4的点表示的数是: ;
⑶ 若将数轴折叠,使得A点与-3表示的点重合,则B点与数 表示的 点重合;
点重合;
⑷ 若数轴上M、N两点之间的距离为2014(M 在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M: N: .
在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M: N: .
查看答案和解析>>
科目:初中数学 来源: 题型:
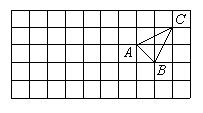
如图,在边长为1的正方形网格中,有一格点△ABC,已知A、B、C三点的坐标分别是A(1,0)、B(2,-1)、C(3,1).
(1) 请在网格图形中画出平面直角坐标系;
(2) 以原点O为位似中心,将△ABC放大2倍,画出放大后的△A′B′C′;
(3) 写出△A′B′C′各顶点的坐标:A′____,B′____,C′ ___;


查看答案和解析>>
科目:初中数学 来源: 题型:
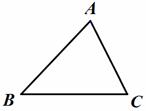
如图,已知锐角△ABC(1)过点A作BC边的垂线MN,交BC于点D(用尺规作图法,保留作图痕迹,不要求写作法);(2)在(1)条件下,若BC=5,AD=4, tan∠BAD=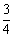 ,求DC的长.
,求DC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com