考点:一次函数图象上点的坐标特征,等腰直角三角形
专题:计算题
分析:(1)设直线y=
x+
与x轴的交点为G,过点A
1,A
2,A
3分别作x轴的垂线,垂足分别为D、E、F,由条件可求得
=
=
,再根据等腰三角形可分别求得A
1D、A
2E、A
3F,可得到A
1,A
2,A
3的坐标;
(2)同(1)的思路,过A
n的作A
nM⊥x轴,同理可求得A
n的坐标.
解答:解:(1)设直线y=
x+
与x轴的交点为G,
令y=0可解得x=-4,
∴G点坐标为(-4,0),
∴OG=4,
如图1,过点A
1,A
2,A
3分别作x轴的垂线,垂足分别为D、E、F,
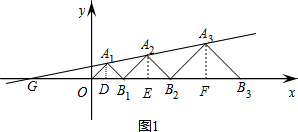
∵△A
1B
1O为等腰直角三角形,
∴A
1D=OD,
又∵点A
1在直线y=
x+
上,
∴
=
,即
=
,
解得A
1D=1=(
)
0,
∴A
1(1,1),OB
1=2,
同理可得
=
,即
,
解得A
2E=
=(
)
1,则OE=OB
1+B
1E=
,
∴A
2(
,
),OB
2=5,
同理可求得A
3F=
=(
)
2,则OF=5+
=
,
∴A
3(
,
);
故答案为:A
1(1,1),A
2(
,
),A
3(
,
);
(2)由(1)可知当A
n时其纵坐标为(
)
n-1,代入直线y=
x+
可求得y=
×(
)
n-1+
,
∴A
n((
)
n-1,
×(
)
n-1+
),
故答案为:((
)
n-1,
×(
)
n-1+
).
点评:本题主要考查等腰三角形的性质和直线上点的坐标特点,根据题意找到点的坐标的变化规律是解题的关键,注意观察数据的变化.

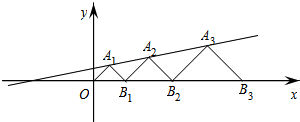 在平面直角坐标系中,点A1,A2,A3和B1,B2,B3分别在直线y=
在平面直角坐标系中,点A1,A2,A3和B1,B2,B3分别在直线y=


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案