
 如图,点A,D在反比例函数y=$\frac{8}{x}$(x>0)的图象上,点A的坐标是(2,4),接AD,过点A作AB⊥AD,交y轴于点B,过点D作DC⊥AD,交x轴于点C,连接BC,四边形ABCD为正方形.
如图,点A,D在反比例函数y=$\frac{8}{x}$(x>0)的图象上,点A的坐标是(2,4),接AD,过点A作AB⊥AD,交y轴于点B,过点D作DC⊥AD,交x轴于点C,连接BC,四边形ABCD为正方形.分析 (1)作AF⊥y轴于点F,根据点A的坐标是(2,4)可知AF=2,OF=4.四边形ABCD是正方形,再由AAS定理得出△AFB≌△BOC,故OB=AF=2,OC=BF=OF-OB=4-2=2,由此可得出结论;
(2)作DE⊥x轴于点E,根据AAS定理可得出△CED≌△BOC,故CE=BO=2,DE=OC=2,OE=OC+CE=2+2=4,由此可得出结论.
解答 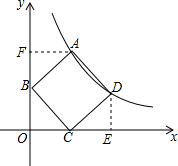 解:(1)作AF⊥y轴于点F,
解:(1)作AF⊥y轴于点F,
∵点A的坐标是(2,4),
∴AF=2,OF=4.
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°.
∵∠BAF+∠ABF=90°,∠OBC+∠ABF=90°,
∴∠BAF=∠OBC,
在△AFB与△BOC中,
∵$\left\{\begin{array}{l}AB=BC\\∠AFB=∠BOC\\∠BAF=∠OBC\end{array}\right.$,
∴△AFB≌△BOC(AAS),
∴OB=AF=2,
∴OC=BF=OF-OB=4-2=2,
∴C(2,0);
(2)作DE⊥x轴于点E,
∵∠BCO+∠DCE=90°,∠EDC+∠DCE=90°,
∴∠BCO=∠EDC.
在△CED与△BOC中,
∵$\left\{\begin{array}{l}BC=CD\\∠BOC=∠CED\\∠BCO=∠EDC\end{array}\right.$,
∴△CED≌△BOC(AAS),
∴CE=BO=2,DE=OC=2,
∴OE=OC+CE=2+2=4,
∴D(4,2).
点评 本题考查的是反比例函数综合题,根据题意作出辅助线,构造出全等三角形是解答此题的关键.


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:解答题
 在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m≤5时为A级,5≤m<10时为B级,10≤m<15时为C级,15≤m<20时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,根据调查数据整理并制作图表如下:
在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m≤5时为A级,5≤m<10时为B级,10≤m<15时为C级,15≤m<20时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,根据调查数据整理并制作图表如下:| m | 频数 | 百分数 |
| A级(0≤m≤5) | 90 | 0.3 |
| B级(5≤m<10) | 120 | a |
| C级(10≤m<15) | b | 0.2 |
| D级(15≤m<20) | 30 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
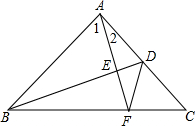 如图所示,在△ABC中,AB=AC,∠BAC=90°,D是AC的中点,AF⊥BD于点E,交BC于点F,连接DF.求证:∠ADB=∠CDF.
如图所示,在△ABC中,AB=AC,∠BAC=90°,D是AC的中点,AF⊥BD于点E,交BC于点F,连接DF.求证:∠ADB=∠CDF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com