
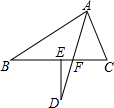
 如图,在△ABC中,∠B=30°,∠C=70°,AD平分∠BAC,交BC于F,DE⊥BC于E,则∠D=20°.
如图,在△ABC中,∠B=30°,∠C=70°,AD平分∠BAC,交BC于F,DE⊥BC于E,则∠D=20°.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
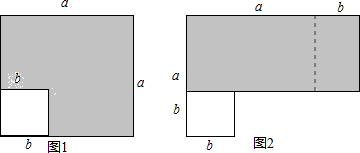
| A. | a<2 | B. | a>2 | C. | a≤2 | D. | a≥2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
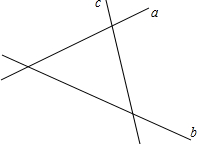 如图,有三条公路a,b,c,为了方便司机休息,路政部门确定修建一个休息站P,使它到三条公路的距离相等.(请用尺规作图,保留作图痕迹,不写作法.)
如图,有三条公路a,b,c,为了方便司机休息,路政部门确定修建一个休息站P,使它到三条公路的距离相等.(请用尺规作图,保留作图痕迹,不写作法.)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A,D在反比例函数y=$\frac{8}{x}$(x>0)的图象上,点A的坐标是(2,4),接AD,过点A作AB⊥AD,交y轴于点B,过点D作DC⊥AD,交x轴于点C,连接BC,四边形ABCD为正方形.
如图,点A,D在反比例函数y=$\frac{8}{x}$(x>0)的图象上,点A的坐标是(2,4),接AD,过点A作AB⊥AD,交y轴于点B,过点D作DC⊥AD,交x轴于点C,连接BC,四边形ABCD为正方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
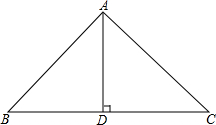 若经过一个三角形某一顶点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形为等腰三角形过该顶点的生成三角形.
若经过一个三角形某一顶点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形为等腰三角形过该顶点的生成三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com