
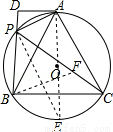
(9分)如图,A,P,B,C是⊙O上的四个点,∠APC=∠BPC=60°,过点A作⊙O的切线交BP的延长线于点D.

(1)求证:△ADP∽△BDA;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)若AD=2,PD=1,求线段BC的长.
(1)证明详见解析;(2) PA+PB=PC,证明详见解析;(3)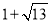 .
.
【解析】
试题分析:(1)首先作⊙O的直径AE,连接PE,利用切线的性质以及圆周角定理得出∠PAD=∠PBA进而得出答案;
(2)首先在线段PC上截取PF=PB,连接BF,进而得出△BPA≌△BFC(AAS),即可得出PA+PB=PF+FC=PC;
(3)利用△ADP∽△BDA,得出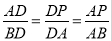 ,求出BP的长,进而得出△ADP∽△CAP,则
,求出BP的长,进而得出△ADP∽△CAP,则 ,则AP2=CPPD求出AP的长,即可得出答案.
,则AP2=CPPD求出AP的长,即可得出答案.
试题解析:(1)证明:作⊙O的直径AE,连接PE,
∵AE是⊙O的直径,AD是⊙O的切线,
∴∠DAE=∠APE=90°,∴∠PAD+∠PAE=∠PAE+∠E=90°,
∴∠PAD=∠E,∵∠PBA=∠E,∴∠PAD=∠PBA,
∵∠PAD=∠PBA,∠ADP=∠BDA,∴△ADP∽△BDA;
(2)PA+PB=PC,
证明:在线段PC上截取PF=PB,连接BF,
∵PF=PB,∠BPC=60°,∴△PBF是等边三角形,
∴PB=BF,∠BFP=60°,∴∠BFC=180°﹣∠PFB=120°,
∵∠BPA=∠APC+∠BPC=120°,∴∠BPA=∠BFC,
在△BPA和△BFC中,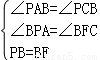 ,
,
∴△BPA≌△BFC(AAS),∴PA=FC,AB=BC,∴PA+PB=PF+FC=PC;
(3)【解析】
∵△ADP∽△BDA,∴ =
=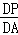 =
=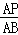 ,
,
∵AD=2,PD=1∴BD=4,AB=2AP,∴BP=BD﹣DP=3,
∵∠APD=180°﹣∠BPA=60°,∴∠APD=∠APC,
∵∠PAD=∠E,∠PCA=∠E,∴PAD=∠PCA,∴△ADP∽△CAP,∴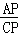 =
=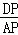 ,
,
∴AP2=CPPD,∴AP2=(3+AP)1,
解得:AP=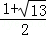 或AP=
或AP= (舍去),∴BC=AB=2AP=1+
(舍去),∴BC=AB=2AP=1+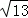 .
.
考点:切线的性质;圆周角定理;全等三角形的判定和性质;相似三角形的判定和性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014-2015学年辽宁省大石桥市八年级上学期段测数学试卷(解析版) 题型:解答题
先化简,再求值:
(1)x(x-1)+2x(x+1)-(3x-1)(2x-5),其中x=2.
(2)若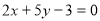 ,求
,求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省南昌市九年级上学期期末终结性测试数学试卷(解析版) 题型:选择题
将等边△ABC绕自身的内心O,顺时针至少旋转n°,就能与自身重合,则n等于( ).
A.60 B.120 C.180 D.360
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省宜昌市兴山县九年级上学期期末调研考试数学试卷(解析版) 题型:选择题
小胡同学的身高为1.6米,某一时刻她在阳光下的影长为2米, 与她邻近的一根旗杆的影长为5米,则这根旗杆的高为( )
A.3米 B.3.6米 C.4米 D.4.8米
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省宜昌市兴山县九年级上学期期末调研考试数学试卷(解析版) 题型:选择题
二次函数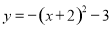 的图像的顶点坐标是( )
的图像的顶点坐标是( )
A.(2,3) B.(2,-3) C.(-2,3) D.(-2,-3)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省广水市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
(5分)广水市为了改善全市中、小学办学条件,计划集中采购一批电子白板和投影机.已知购买2块电子白板比购买3台投影机多4000元,购买4块电子白板和3台投影机共需44000元.问购买一块电子白板和一台投影机各需要多少元?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省商丘市九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上.将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
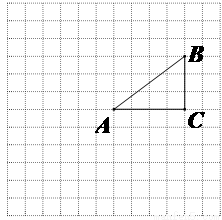
(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过的区域的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省梅州市九年级上学期第一次月考数学试卷(解析版) 题型:选择题
顺次连接菱形四边中点所得的四边形一定是( ).
A.梯形 B.矩形 C.菱形 D.正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com