练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

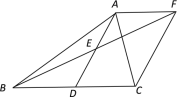
    【题目】如图，在△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交BE的延长线于F，且AF=DC，连接CF．

    （1）求证：D是BC的中点；

    （2）如果AB=AC，试判断四边形ADCF的形状，并证明你的结论．

    【答案】（1）见解析；（2）四边形是矩形，证明见解析.

    【解析】

    （1）因为AF∥BC，E为AD的中点，即可根据AAS证明△AEF≌△DEC，得到．又故有BD=DC；
    （2）由（1）知，AF=DC且AF∥DC，可得四边形AFDC是平行四边形，又因为，是的中点，得到．根据有一个角是直角的平行四边形是矩形进行判定．

    （1）证明：， ．

    是的中点，．

    又，

    ．

    ．

    ， ．即是的中点．

    （2）解：四边形是矩形，

    证明：，，

    四边形是平行四边形．

    ，是的中点，

    ．

    即． 四边形是矩形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

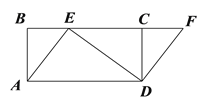
    【题目】如图，四边形ABCD是矩形，点E在BC边上，点F在BC延长线上，且∠CDF =∠BAE．

    （1）求证：四边形AEFD是平行四边形；

    （2）若DF=3，DE=4，AD=5，求CD的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现代互联网技术的广泛应用，催生了快递行业的高速发展，据调查，某家快递公司，今年三月份与五月份完成投递的快件总件数分别是5万件和万件，现假定该公司每月投递的快件总件数的增长率相同．

    求该公司投递快件总件数的月平均增长率；

    如果平均每人每月可投递快递万件，那么该公司现有的16名快递投递员能否完成今年6月份的快递投递任务？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知∠MON=140°，∠AOC与∠BOC互余，OC平分∠MOB，

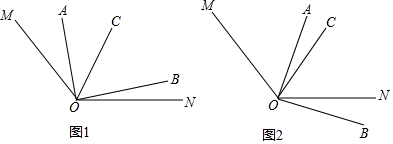
    （1）在图1中，若∠AOC=40°，则∠BOC= °，∠NOB= °．

    （2）在图1中，设∠AOC=α，∠NOB=β，请探究α与β之间的数量关系（ 必须写出推理的主要过程，但每一步后面不必写出理由）；

    （3）在已知条件不变的前提下，当∠AOB绕着点O顺时针转动到如图2的位置，此时α与β之间的数量关系是否还成立？若成立，请说明理由；若不成立，请直接写出此时α与β之间的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

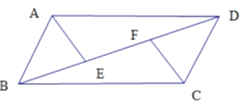
    【题目】如图，在口ABCD中，点E、F是对角线BD上的两点，且BF=DE，连接AE、CF.

    .求证：AE//CF.

    【答案】证明见解析

    【解析】试题分析：根据平行四边形的性质可得AD=CB，∠ADE=∠CBF，利用SAS判定△ADE≌△CBF，根据全等三角形的性质即可得∠AED=∠BFC，所以AE∥CF.

    试题解析：

    ∵四边形ABCD是平行四边形，

    ∴AD=CB，AD∥CB，

    ∴∠ADE=∠CBF，

    又∵DE=BF，

    ∴△ADE≌△CBF，

    ∴∠AED=∠BFC，

    ∴AE∥CF.

    【题型】解答题
    【结束】
    22

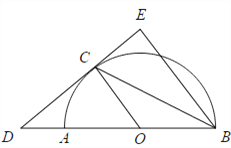
    【题目】如图，已知是 的直径，CD与 相切于C， .

    （1）求证：BC 是的平分线.

    （2）若DC=8， 的半径OA=6，求CE的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

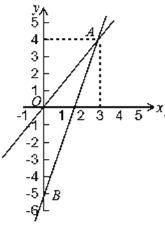
    【题目】如图，一个正比例函数与一个一次函数的图象交于点A（3，4），其中一次函数与y轴交于B点，且OA＝OB．

    （1）求这两个函数的表达式；

    （2）求△AOB的面积S．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司为了了解员工每人所创年利润情况，公司从各部抽取部分员工对每年所创年利润情况进行统计，并绘制如图1，图2统计图．

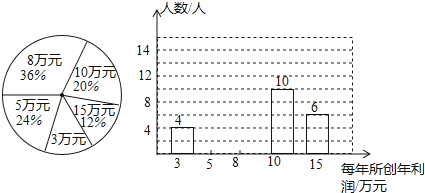
    （1）求抽取员工总人数，并将图补充完整；

    （2）每人所创年利润的众数是 ，每人所创年利润的中位数是 ，平均数是 ；

    （3）若每人创造年利润10万元及（含10万元）以上为优秀员工，在公司1200员工中有多少可以评为优秀员工？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】工业园区某机械厂的一个车间主要负责生产螺丝和螺母，该车间有工人44人，其中女生人数比男生人数的倍少人，每个工人平均每天可以生产螺丝个或者螺母个

    （1）该车间有男生、女生各多少人？

    （2）已知一个螺丝与两个螺母配套，为了使每天生产的螺丝螺母恰好配套，应该分配多少工人负责生产螺丝，多少工人负责生产螺母？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在一张平行四边形纸片ABCD中，画一个菱形，甲、乙两位同学的画法如下：甲：以B，A为圆心，AB长为半径作弧，分别交BC，AD于点E，F，则四边形ABEF为菱形；乙：作∠A，∠B的平分线AE，BF，分别交BC于点E，交AD于点F，则四边形ABEF是菱形；关于甲、乙两人的画法，下列判断正确的是（　　）

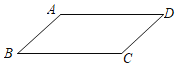
    A. 仅甲正确B. 仅乙正确

    C. 甲、乙均正确D. 甲、乙均错误

    查看答案和解析>>

    同步练习册答案