
解方程:x(2x﹣3)=3﹣2x.
【考点】解一元二次方程-因式分解法.
【分析】首先移项得到x(2x﹣3)+(2x﹣3)=0,然后提取公因式(2x﹣3),最后解两个一元一次方程即可.
【解答】解:∵x(2x﹣3)=3﹣2x,
∴x(2x﹣3)+(2x﹣3)=0,
∴(2x﹣3)(x+1)=0,
∴2x﹣3=0或x+1=0,
∴x1=﹣1,x2=
 .
.
【点评】本题主要考查了因式分解法解一元二次方程的知识,解答本题的关键是掌握因式分解法解一元二次方程的一般步骤:①移项,使方程的右边化为零;②将方程的左边分解为两个一次因式的乘积;③令每个因式分别为零,得到两个一元一次方程;④解这两个一元一次方程,它们的解就都是原方程的解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
如图,将四根长度相等的细木条首尾相连,用钉子钉成四边形ABCD,转动这个四边形,使它形状改变,当AB=2,∠B=60°时,AC等于( )
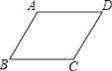

A.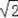
 B.2 C.
B.2 C.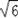
 D.2
D.2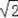

查看答案和解析>>
科目:初中数学 来源: 题型:
.如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,AE∥CD,CE∥AB,连接DE交AC于点O.
(1)证明:四边形ADCE为菱形;
(2)证明:DE=BC.


查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,若将抛物线y=2x2分别向上、向右平移2个单位,则新抛物线的解析式是( )
A.y=2(x﹣2)2+2 B.y=2(x+2)2﹣2 C.y=2(x﹣2)2﹣2 D.y=2(x+2)2+2
查看答案和解析>>
科目:初中数学 来源: 题型:
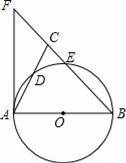
如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2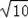
 ,CE:EB=1:4,求CE的长.
,CE:EB=1:4,求CE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com