
【题目】“金山银山,不如绿水青山”.鄂尔多斯市某旗区不断推进“森林城市”建设,今春种植四类树苗,园林部门从种植的这批树苗中随机抽取了4000棵,将各类树苗的种植棵数绘制成扇形统计图,将各类树苗的成活棵数绘制成条形统计图,经统计松树和杨树的成活率较高,且杨树的成活率为97%,根据图表中的信息解答下列问题:
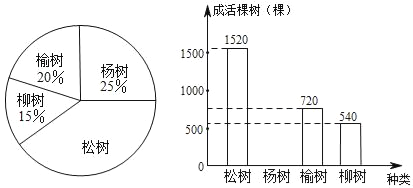
(1)扇形统计图中松树所对的圆心角为 度,并补全条形统计图.
(2)该旗区今年共种树32万棵,成活了约多少棵?
(3)园林部门决定明年从这四类树苗中选两类种植,请用列表法或树状图求恰好选到成活率较高的两类树苗的概率.(松树、杨树、榆树、柳树分别用A,B,C,D表示)
【答案】(1)144°,见解析;(2)300000棵,(3)![]() ,见解析.
,见解析.
【解析】
(1)根据题意列式计算,补全条形统计图即可;
(2)根据题意列式计算即可求出;
(3)画树状图得出所有等可能的情况数,找出选到成活率较高的两类树苗的情况数,即可求出所求的概率.
解:(1)扇形统计图中松树所对的圆心角为360°×(1﹣20%﹣15%﹣25%)=144°,
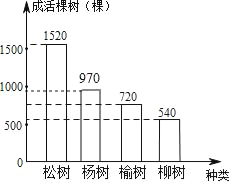
杨树的棵数=4000×25%×97%=970(棵),
补全条形统计图如图所示;
(2)320000×![]() ×100%=300000(棵),
×100%=300000(棵),
答:成活了约300000棵;
(3)
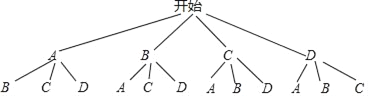
所有等可能的情况有12种,其中恰好选到成活率较高的两类树苗有2种,
∴恰好选到成活率较高的两类树苗的概率=![]() =
=![]() .
.
故答案为:(1)144°,见解析;(2)300000棵,(3)![]() ,见解析.
,见解析.


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
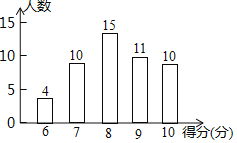
【题目】为了了解居民的环保意识,社区工作人员在光明小区随机抽取了若干名居民开展主题为“打赢蓝天保卫战”的环保知识有奖问答活动,并用得到的数据绘制了如图条形统计图(得分为整数,满分为10分,最低分为6分)
请根据图中信息,解答下列问题:
(1)本次调查一共抽取了 名居民;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)社区决定对该小区500名居民开展这项有奖问答活动,得10分者设为“一等奖”,请你根据调查结果,帮社区工作人员估计需准备多少份“一等奖”奖品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线BD上,转轴B到地面的距离BD=3m.小亮在荡秋千过程中,当秋千摆动到最高点A时,测得点A到BD的距离AC=2m,点A到地面的距离AE=1.8m;当他从A处摆动到A′处时,有A'B⊥AB.
(1)求A′到BD的距离;
(2)求A′到地面的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由菜鸟网络打造的一个仓库有相同数量的工人和机器人,均为x名(其中x>5),平时每天都只工作8小时,每名机器人每小时加工包裹(分、拣、包装一体化)的数量是每名工人每小时加工包裹数量的2倍.随着“春节”临近,人工短缺,寄年货的包裹增多,公司决定再增加2名机器人,且将机器人每天工作时间延长至12小时,并对每名机器人进行升级改造,让现在每名机器人每小时加工包裹的数量在原有基础上增加x个,结果现在所有机器人每天加工包裹的数量是所有工人平时每天加工包裹数量的6倍,则该仓库平时一天加工______个包裹.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于![]() 长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.

(1)四边形ABEF是_______;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为________,∠ABC=________°.(直接填写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D.
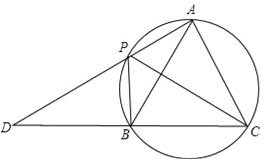
(1)求证:△ABC是等边三角形;
(2)若∠PAC=90°,AB=![]() ,求PD的长.
,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
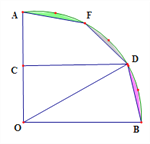
【题目】如图,扇形纸片AOB中,已知∠AOB=90,OA=6,取OA的中点C,过点C作DC⊥OA交![]() 于点D,点F是
于点D,点F是![]() 上一点.若将扇形BOD沿OD翻折,点B恰好与点F重合,用剪刀沿着线段BD、DF、FA依次剪下,则剩下的纸片(阴影部分)面积是______________.
上一点.若将扇形BOD沿OD翻折,点B恰好与点F重合,用剪刀沿着线段BD、DF、FA依次剪下,则剩下的纸片(阴影部分)面积是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
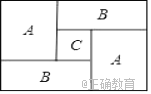
【题目】如图,一个长方形运动场被分隔成![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 共
共![]() 个区,
个区, ![]() 区是边长为
区是边长为![]() 的正方形,
的正方形, ![]() 区是边长为
区是边长为![]() 的正方形.
的正方形.
(1)列式表示每个![]() 区长方形场地的周长,并将式子化简;
区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果![]() ,
, ![]() ,求整个长方形运动场的面积.
,求整个长方形运动场的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=ax+b过一,二,四象限,且过(6,0),则关于二次函数y=ax2+bx+1的以下说法:①图象与x轴有两个交点;②a<0,b>0;③当x=3时函数有最小值;④若存在一个实数m,当x≤m时,y随x的增大而增大,则m≤3.其中正确的是( )
A. ①②B. ①②③C. ①②④D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com